Corrigé de l'exercice 3 de maths du bac S de juin 2011 en Polynésie
Cacher les corrigés
Partie A : Restitution organisée de connaissances
Dans le sujet original on demandait aux élèves de montrer la formule d'intégration par parties. Cette méthode
d'intégration ne figure plus dans les nouveaux programmes à partir de la rentrée 2012.
Partie B
On considère la fonction définie sur
définie sur 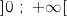 par
par
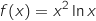
 en
en  .
.
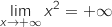 et
et 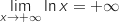 , donc par produit
, donc par produit 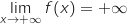 .
.
 sur
sur 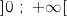 .
.
La fonction  est dérivable sur
est dérivable sur  et
et 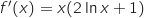 .
Sur
.
Sur 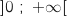 , le signe de
, le signe de  est le même que celui de
est le même que celui de 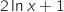 .
On résout :
.
On résout : 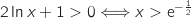 .
On a de même
.
On a de même 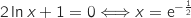 et
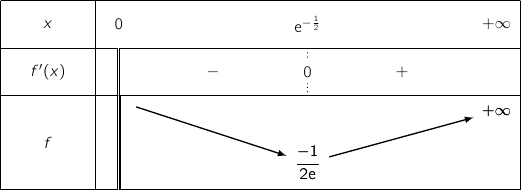
et 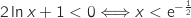 On en déduit le tableau de variations :
On en déduit le tableau de variations :
 est dérivable sur
est dérivable sur  et
et 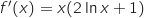 .
Sur
.
Sur 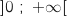 , le signe de
, le signe de  est le même que celui de
est le même que celui de 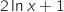 .
On résout :
.
On résout : 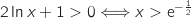 .
On a de même
.
On a de même 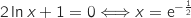 et
et 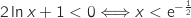 On en déduit le tableau de variations :
On en déduit le tableau de variations :

2. Pour cette question, toute trace de recherche, même incomplète, sera prise en compte dans l'évaluation. Démontrer qu'il existe une tangente unique à la courbe
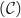 passant par O. Préciser une équation de cette tangente.
passant par O. Préciser une équation de cette tangente.
L'équation réduite de la tangente au point d'abscisse  est :
est : 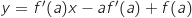 .
Dire que la tangente passe par O revient à dire que l'ordonnée à l'origine est nulle soit :
.
Dire que la tangente passe par O revient à dire que l'ordonnée à l'origine est nulle soit :
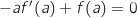 .
On obtient l'équation :
.
On obtient l'équation : 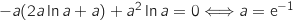 .
Donc il existe une unique tangente passant par O : c'est la tangente au point d'abscisse
.
Donc il existe une unique tangente passant par O : c'est la tangente au point d'abscisse 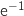 .
On a
.
On a 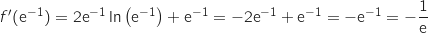 .
Donc l'équation de cette tangente est
.
Donc l'équation de cette tangente est 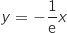 .
.
 est :
est : 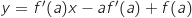 .
Dire que la tangente passe par O revient à dire que l'ordonnée à l'origine est nulle soit :
.
Dire que la tangente passe par O revient à dire que l'ordonnée à l'origine est nulle soit :
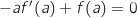 .
On obtient l'équation :
.
On obtient l'équation : 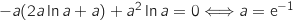 .
Donc il existe une unique tangente passant par O : c'est la tangente au point d'abscisse
.
Donc il existe une unique tangente passant par O : c'est la tangente au point d'abscisse 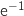 .
On a
.
On a 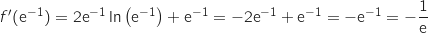 .
Donc l'équation de cette tangente est
.
Donc l'équation de cette tangente est 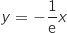 .
.
Dans le sujet initial la fin de l'exercice nécessitait l'utilisation d'un intégration par parties qui est désormais hors programme.
