Corrigé de l'exercice 4 de maths du bac S de juin 2011 en Polynésie
Cacher les corrigés
On considère le cube ABCDEFGH de côté 1 représenté ci-dessous.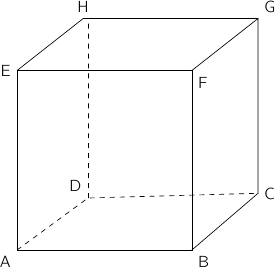
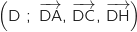 .
On note K le point de coordonnées
.
On note K le point de coordonnées 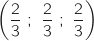 .
.
Partie A
Dans le sujet original la première question de la partie A consistait à calculer les coordonnées de K défini
comme barycentre de points pondérés.
2. Montrer que les droites (EK) et (DF) sont orthogonales.
Le point E a pour coordonnées : E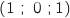 .
On a les coordonnées des vecteurs :
.
On a les coordonnées des vecteurs : 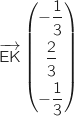 et
et
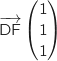 .
On calcule le produit scalaire :
.
On calcule le produit scalaire :
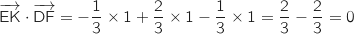 Le produit scalaire étant nul, on en déduit que
Le produit scalaire étant nul, on en déduit que 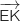 et
et 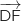 sont orthogonaux et donc les droites (EK) et (EF) également.
sont orthogonaux et donc les droites (EK) et (EF) également.
3. Calculer la distance EK.
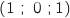 .
On a les coordonnées des vecteurs :
.
On a les coordonnées des vecteurs : 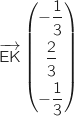 et
et
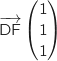 .
On calcule le produit scalaire :
.
On calcule le produit scalaire :
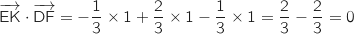 Le produit scalaire étant nul, on en déduit que
Le produit scalaire étant nul, on en déduit que 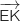 et
et 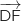 sont orthogonaux et donc les droites (EK) et (EF) également.
sont orthogonaux et donc les droites (EK) et (EF) également.
On utilise la formule de la distance :
EK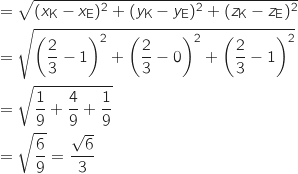
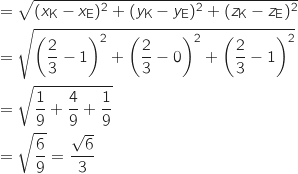
Partie B
Soit M un point du segment [HG]. On note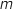 = HM (
= HM (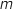 est donc un réel appartenant à
est donc un réel appartenant à  ).
1. Montrer que, pour tout réel
).
1. Montrer que, pour tout réel 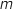 appartenant à l'intervalle
appartenant à l'intervalle  , le volume du tétraèdre EMFD, en unités de volume, est égal à
, le volume du tétraèdre EMFD, en unités de volume, est égal à  .
.
On considère le tétraèdre avec la base EMF, dans ce cas la hauteur est toujours égale à 1.
En outre on remarque que le triangle EMF a toujours une aire qui vaut  (on calcule l'aire avec la base [EF] et dans ce cas la hauteur correspondante est toujours de longueur 1).
Donc le volume du tétraèdre est toujours égal à
(on calcule l'aire avec la base [EF] et dans ce cas la hauteur correspondante est toujours de longueur 1).
Donc le volume du tétraèdre est toujours égal à 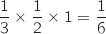 .
.
2. Montrer qu'une équation cartésienne du plan (MFD) est
 (on calcule l'aire avec la base [EF] et dans ce cas la hauteur correspondante est toujours de longueur 1).
Donc le volume du tétraèdre est toujours égal à
(on calcule l'aire avec la base [EF] et dans ce cas la hauteur correspondante est toujours de longueur 1).
Donc le volume du tétraèdre est toujours égal à 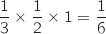 .
.
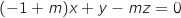
Les points M, D et F ne sont jamais alignés donc il définissent toujours un plan, pour montrer que l'équation proposée est une équation de (MFD), il suffit de montrer que les coordonnées
de M, D et F vérifient l'équation.
Pour M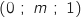 :
: 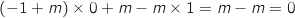 , donc c'est bon.
Pour F
, donc c'est bon.
Pour F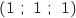 :
: 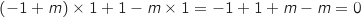 , donc c'est bon.
Pour D
, donc c'est bon.
Pour D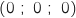 :
: 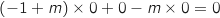 , donc c'est bon.
, donc c'est bon.
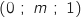 :
: 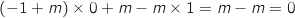 , donc c'est bon.
Pour F
, donc c'est bon.
Pour F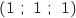 :
: 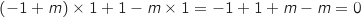 , donc c'est bon.
Pour D
, donc c'est bon.
Pour D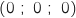 :
: 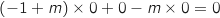 , donc c'est bon.
, donc c'est bon.
La notion de distance d'un point à un plan ne figure plus au programme depuis la rentrée 2012. La fin de cet exercice
peut tout de même encore être proposée aux élèves à condition de préciser cette notion.
3. Etant donné un point A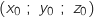 et un plan
et un plan  d'équation
d'équation 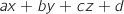 , la distance
de A à
, la distance
de A à  est donnée par la formule :
est donnée par la formule :
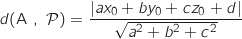
 , c'est également la plus petite
distance de A au plan
, c'est également la plus petite
distance de A au plan  .
On note
.
On note 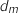 la distance du point E au plan (MFD).
a. Montrer que, pour tout réel
la distance du point E au plan (MFD).
a. Montrer que, pour tout réel 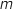 appartenant à l'intervalle
appartenant à l'intervalle  :
:
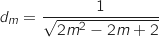
On utilise la formule de la distance d'un point à un plan, avec E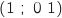 et l'équation du plan de la question précédente ce qui donne :
et l'équation du plan de la question précédente ce qui donne :
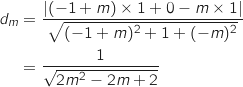
b. Déterminer la position de M sur le segment [HG] pour laquelle la distance 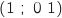 et l'équation du plan de la question précédente ce qui donne :
et l'équation du plan de la question précédente ce qui donne :
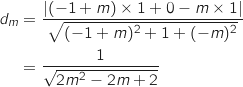
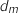 est maximale.
est maximale.
On remarque que 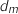 est maximale quand
est maximale quand 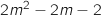 est minimale.
Comme l'expression est un trinôme du second degré on sait directement que sont minimum est atteint pour
est minimale.
Comme l'expression est un trinôme du second degré on sait directement que sont minimum est atteint pour 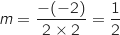 (formule
(formule 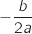 ).
Donc la distance
).
Donc la distance 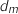 est maximale lorsque M est au milieu du segment [HG].
est maximale lorsque M est au milieu du segment [HG].
c. En déduire que lorsque la distance 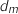 est maximale quand
est maximale quand 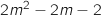 est minimale.
Comme l'expression est un trinôme du second degré on sait directement que sont minimum est atteint pour
est minimale.
Comme l'expression est un trinôme du second degré on sait directement que sont minimum est atteint pour 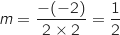 (formule
(formule 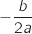 ).
Donc la distance
).
Donc la distance 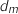 est maximale lorsque M est au milieu du segment [HG].
est maximale lorsque M est au milieu du segment [HG].
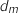 est maximale, le point K est le projeté orthogonal de E sur le plan (MFD).
est maximale, le point K est le projeté orthogonal de E sur le plan (MFD).
La distance maximale obtenue pour 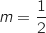 vaut :
vaut : 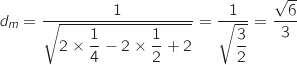 .
Donc
.
Donc 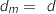 (E,MFD)
(E,MFD) EK, or la distance de E à (MFD) est la plus courte distance séparant E d'un point du plan qui ne peut donc être que K. D'autre part on sait que cette distance est aussi la
distance séparant E de son projeté orthogonal sur le plan, donc K est le projeté orthogonal de E sur le plan (MFD).
EK, or la distance de E à (MFD) est la plus courte distance séparant E d'un point du plan qui ne peut donc être que K. D'autre part on sait que cette distance est aussi la
distance séparant E de son projeté orthogonal sur le plan, donc K est le projeté orthogonal de E sur le plan (MFD).
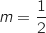 vaut :
vaut : 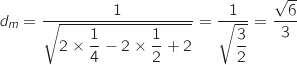 .
Donc
.
Donc 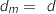 (E,MFD)
(E,MFD) EK, or la distance de E à (MFD) est la plus courte distance séparant E d'un point du plan qui ne peut donc être que K. D'autre part on sait que cette distance est aussi la
distance séparant E de son projeté orthogonal sur le plan, donc K est le projeté orthogonal de E sur le plan (MFD).
EK, or la distance de E à (MFD) est la plus courte distance séparant E d'un point du plan qui ne peut donc être que K. D'autre part on sait que cette distance est aussi la
distance séparant E de son projeté orthogonal sur le plan, donc K est le projeté orthogonal de E sur le plan (MFD).
