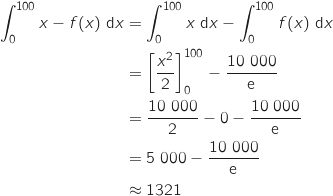Corrigé de l'exercice 1 du bac S de maths de juin 2012 en Polynésie
Cacher les corrigés
Le plan est rapporté à un repère orthonormal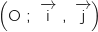 .
On considère les points B
.
On considère les points B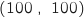 et C
et C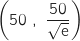 et la droite (D) d'équation
et la droite (D) d'équation 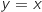 .
On note
.
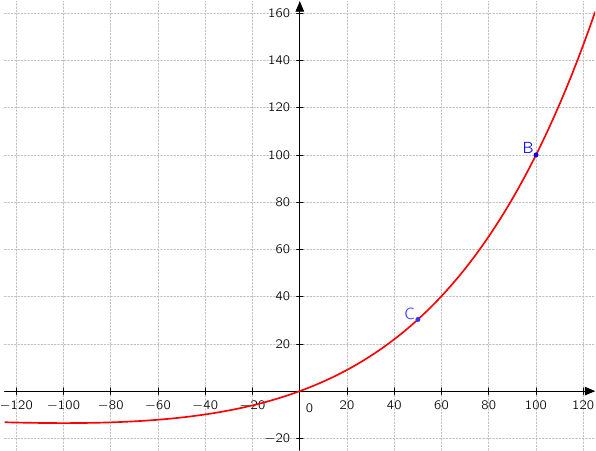
On note  la fonction définie sur
la fonction définie sur  dont la courbe représentative, notée
dont la courbe représentative, notée  , est donnée ci-dessous :
, est donnée ci-dessous :
 et
et  tels que :
tels que :
- pour tout
 réel,
réel, 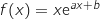
- les points B et C appartiennent à la courbe
 .
.
1.a. Montrer que le couple
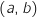 est solution du système :
est solution du système :
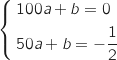
La courbe de la fonction  passe par le point B, donc
passe par le point B, donc 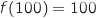 , ce qui donne :
, ce qui donne :
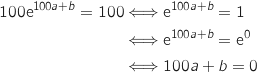 De même la courbe
De même la courbe  passe par C, donc
passe par C, donc 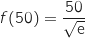 , donc on a :
, donc on a :
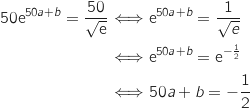 Donc le couple
Donc le couple 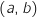 est bien solution du système proposé.
est bien solution du système proposé.
 passe par le point B, donc
passe par le point B, donc 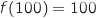 , ce qui donne :
, ce qui donne :
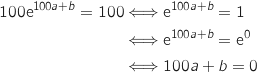 De même la courbe
De même la courbe  passe par C, donc
passe par C, donc 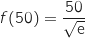 , donc on a :
, donc on a :
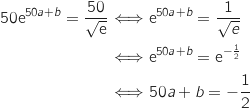 Donc le couple
Donc le couple 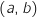 est bien solution du système proposé.
est bien solution du système proposé.
b. En déduire que pour tout
 réel,
réel, 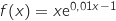 .
.
On résout le système précédent pour déterminer  et
et  .
.
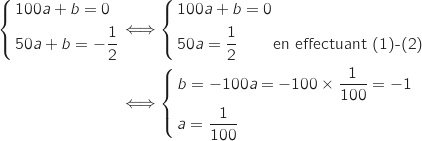 Donc on a bien
Donc on a bien 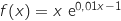 .
.
2. Déterminer la limite de  et
et  .
.
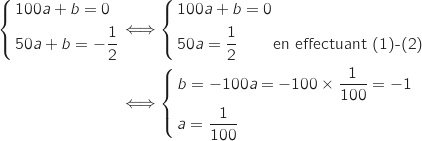 Donc on a bien
Donc on a bien 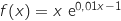 .
.
 en
en  .
.
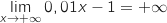 et par composée
et par composée 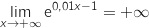 .
Pour finir, par produit :
.
Pour finir, par produit : 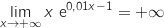 .
.
 réel
réel 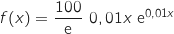 .
.
Pour tout réel  , on a :
, on a :
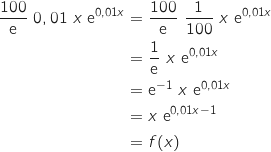
b. En déduire la limite de  , on a :
, on a :
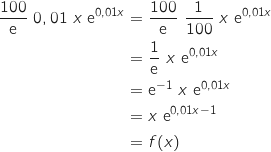
 en
en  .
.
On utilise l'expression précédente de 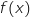 et on pose
et on pose 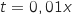 .
.
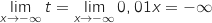 , donc on a :
, donc on a :
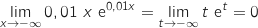 (par croissances comparées).
Finalement en multipliant par
(par croissances comparées).
Finalement en multipliant par 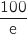 ,
, 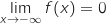 .
.
4. Etudier les variations de la fonction 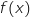 et on pose
et on pose 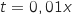 .
.
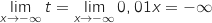 , donc on a :
, donc on a :
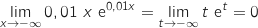 (par croissances comparées).
Finalement en multipliant par
(par croissances comparées).
Finalement en multipliant par 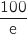 ,
, 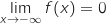 .
.
 . On donnera le tableau de variations complet.
. On donnera le tableau de variations complet.
La fonction  est dérivable sur
est dérivable sur  .
.
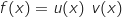 avec :
avec :
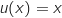
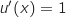
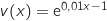
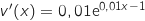 En utilisant la formule de dérivation d'un produit on obtient :
En utilisant la formule de dérivation d'un produit on obtient :
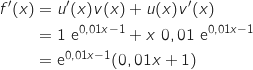 Pour tout
Pour tout  , le signe de la dérivée est le même que celui de
, le signe de la dérivée est le même que celui de 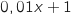 .
Ce binôme du premier degré s'annule pour
.
Ce binôme du premier degré s'annule pour 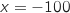 et on a le tableau de variations :
et on a le tableau de variations :
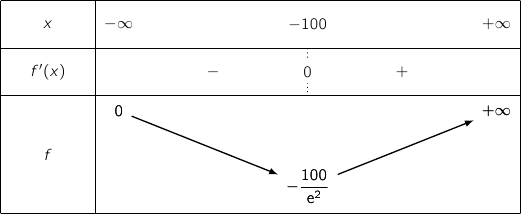
Détail du calcul de 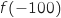
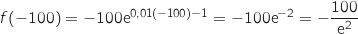 .
.
5. Etudier la position relative de la courbe  est dérivable sur
est dérivable sur  .
.
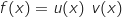 avec :
avec :
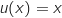
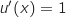
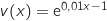
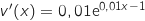 En utilisant la formule de dérivation d'un produit on obtient :
En utilisant la formule de dérivation d'un produit on obtient :
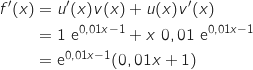 Pour tout
Pour tout  , le signe de la dérivée est le même que celui de
, le signe de la dérivée est le même que celui de 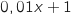 .
Ce binôme du premier degré s'annule pour
.
Ce binôme du premier degré s'annule pour 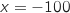 et on a le tableau de variations :
et on a le tableau de variations :

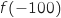
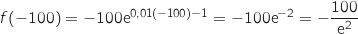 .
.
 et de la droite (D).
et de la droite (D).
Pour faire cette étude on regarde le signe de 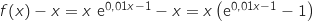 .
Etudions le signe de
.
Etudions le signe de 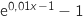 , en résolvant, par exemple,
, en résolvant, par exemple, 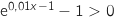 .
.
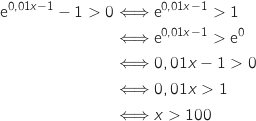 On a de même
On a de même 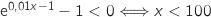 et
et 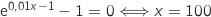 .
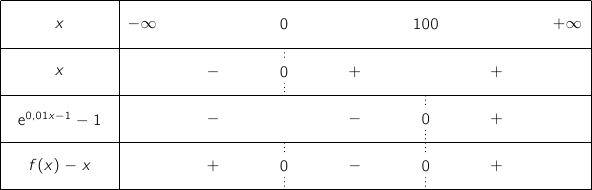
Du coup on a le tableau de signes :
.
Du coup on a le tableau de signes :
On en déduit que :
6.a. On admet que 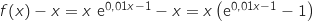 .
Etudions le signe de
.
Etudions le signe de 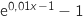 , en résolvant, par exemple,
, en résolvant, par exemple, 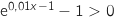 .
.
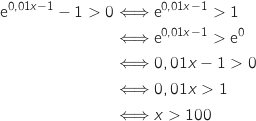 On a de même
On a de même 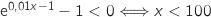 et
et 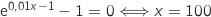 .
Du coup on a le tableau de signes :
.
Du coup on a le tableau de signes :

- pour
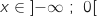 , la courbe
, la courbe 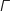 est au dessus de (D),
est au dessus de (D),
- pour
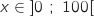 , la courbe
, la courbe 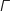 est en dessous de (D),
est en dessous de (D),
- pour
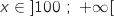 , la courbe
, la courbe 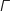 est au dessus de (D),
est au dessus de (D),
- pour
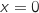 et pour
et pour 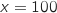 , les courbes
, les courbes  et (D) se coupent.
et (D) se coupent.
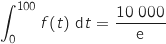 .
.
Dans le sujet original, les élèves doivent calculer cette intégrale en utilisant une intégration par parties.
Cette méthode d'intégration n'est plus au programme à compter de la rentrée 2012.
b. On désigne par A l'aire, en unités d'aire, du domaine du plan délimité par les droites d'équations 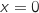 et
et 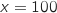 , la droite (D) et la courbe
, la droite (D) et la courbe  .
Calculer A.
.
Calculer A.
On a vu que sur 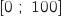 , la courbe
, la courbe  est située en dessous de (D), donc l'aire du domaine en unités d'aire vaut :
est située en dessous de (D), donc l'aire du domaine en unités d'aire vaut :
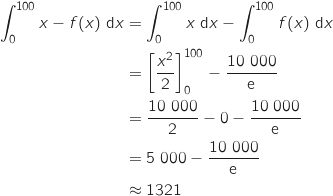
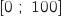 , la courbe
, la courbe  est située en dessous de (D), donc l'aire du domaine en unités d'aire vaut :
est située en dessous de (D), donc l'aire du domaine en unités d'aire vaut :