Corrigé de l'exercice 3 du bac S de maths de juin 2012 en Polynésie
Cacher les corrigés
Partie A
On considère l'algorithme suivant : Les variables sont le réel U et les entiers k et N. Entrée Saisir le nombre entier naturel non nul N Traitement Affecter à U la valeur 0 Pour k allant de 0 à N-1 Affecter à U la valeur 3U-2k+3 Fin pour Sortie Afficher U Quel est l'affichage en sortie lorsque N=3 ?
Pour N=3, la boucle est executée 3 fois (k prend successivement les valeurs 0, 1 et 2).
- Itération 1 : U
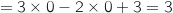
- Itération 2 : U
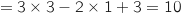
- Itération 3 : U
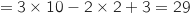
Partie B
On considère la suite définie par
définie par 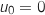 et, pour tout entier naturel
et, pour tout entier naturel  ,
, 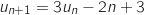 .
1. Calculer
.
1. Calculer 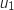 et
et 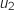 .
.
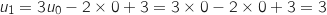
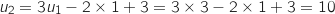
2.a. Démontrer par récurrence que, pour tout entier naturel
 ,
, 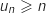 .
.
La propriété à montrer pour tout entier naturel  est
est  : "
: " 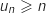 ".
Initialisation
".
Initialisation
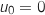 et on a
et on a 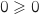 , donc
, donc 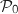 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang  , c'est à dire que :
, c'est à dire que : 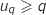 .
On cherche à montrer, qu'alors,
.
On cherche à montrer, qu'alors,  est vraie.
On part de l'hypothèse de récurrence :
est vraie.
On part de l'hypothèse de récurrence :
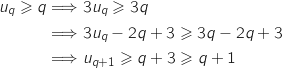 Donc
Donc  est vraie.
Ainsi la propriété est initialisée au rang 0 et elle héréditaire, donc selon le principe de récurrence elle est vraie pour tout entier naturel
est vraie.
Ainsi la propriété est initialisée au rang 0 et elle héréditaire, donc selon le principe de récurrence elle est vraie pour tout entier naturel  .
.
b. En déduire la limite de la suite  est
est  : "
: " 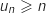 ".
Initialisation
".
Initialisation
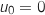 et on a
et on a 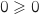 , donc
, donc 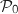 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang  , c'est à dire que :
, c'est à dire que : 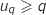 .
On cherche à montrer, qu'alors,
.
On cherche à montrer, qu'alors,  est vraie.
On part de l'hypothèse de récurrence :
est vraie.
On part de l'hypothèse de récurrence :
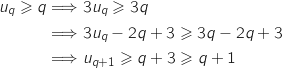 Donc
Donc  est vraie.
Ainsi la propriété est initialisée au rang 0 et elle héréditaire, donc selon le principe de récurrence elle est vraie pour tout entier naturel
est vraie.
Ainsi la propriété est initialisée au rang 0 et elle héréditaire, donc selon le principe de récurrence elle est vraie pour tout entier naturel  .
.
 .
.
On a 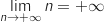 et pour tout entier naturel
et pour tout entier naturel  ,
, 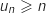 ,
donc par comparaison
,
donc par comparaison 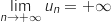 .
.
3. Démontrer que la suite 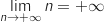 et pour tout entier naturel
et pour tout entier naturel  ,
, 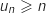 ,
donc par comparaison
,
donc par comparaison 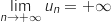 .
.
 est croissante.
est croissante.
Pour tout entier naturel  , on a :
, on a :
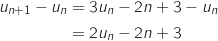 Comme pour tout entier naturel
Comme pour tout entier naturel  on a vu que
on a vu que 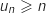 il vient :
il vient :
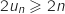 , puis
, puis 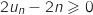 et enfin
et enfin 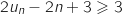 .
Donc
.
Donc 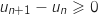 ce qui prouve que la suite
ce qui prouve que la suite  est croissante.
est croissante.
4. Soit la suite  , on a :
, on a :
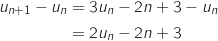 Comme pour tout entier naturel
Comme pour tout entier naturel  on a vu que
on a vu que 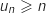 il vient :
il vient :
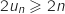 , puis
, puis 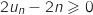 et enfin
et enfin 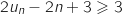 .
Donc
.
Donc 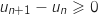 ce qui prouve que la suite
ce qui prouve que la suite  est croissante.
est croissante.
 définie, pour tout entier naturel
définie, pour tout entier naturel  , par
, par 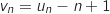 .
a. Démontrer que la suite
.
a. Démontrer que la suite  est une suite géométrique.
est une suite géométrique.
Pour tout entier naturel  , on a :
, on a :
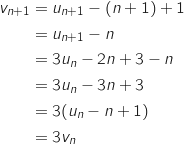 Donc la suite
Donc la suite  est une suite géométrique de raison 3 et de premier terme
est une suite géométrique de raison 3 et de premier terme 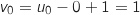 .
.
b. En déduire, que pour tout entier naturel  , on a :
, on a :
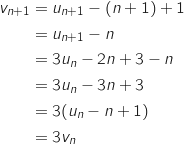 Donc la suite
Donc la suite  est une suite géométrique de raison 3 et de premier terme
est une suite géométrique de raison 3 et de premier terme 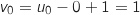 .
.
 ,
, 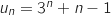 .
.
En utilisant la question précédente on a :
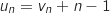 avec
avec 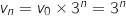 (formule explicite de la suite géométrique).
D'où
(formule explicite de la suite géométrique).
D'où 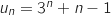 .
.
5. Soit 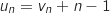 avec
avec 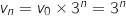 (formule explicite de la suite géométrique).
D'où
(formule explicite de la suite géométrique).
D'où 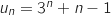 .
.
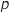 un entier naturel non nul.
a. Pourquoi peut-on affirmer qu'il existe au moins un entier
un entier naturel non nul.
a. Pourquoi peut-on affirmer qu'il existe au moins un entier 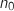 tel que, pour tout
tel que, pour tout 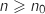 ,
, 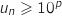 ?
?
La suite  diverge vers
diverge vers  donc par définition de la limite étant donné un réel M quelconque, tous les termes de la suite
donc par définition de la limite étant donné un réel M quelconque, tous les termes de la suite  sont
supérieurs à M à partir d'un certain rang. En prenant M
sont
supérieurs à M à partir d'un certain rang. En prenant M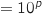 on peut exprimer cela par l'existence d'au moins un entier
on peut exprimer cela par l'existence d'au moins un entier 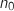 tel que pour tout
tel que pour tout 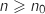 ,
, 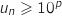 .
.
On s'intéresse maintenant au plus petit entier  diverge vers
diverge vers  donc par définition de la limite étant donné un réel M quelconque, tous les termes de la suite
donc par définition de la limite étant donné un réel M quelconque, tous les termes de la suite  sont
supérieurs à M à partir d'un certain rang. En prenant M
sont
supérieurs à M à partir d'un certain rang. En prenant M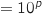 on peut exprimer cela par l'existence d'au moins un entier
on peut exprimer cela par l'existence d'au moins un entier 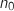 tel que pour tout
tel que pour tout 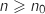 ,
, 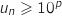 .
.
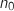 .
b. Justifier que
.
b. Justifier que 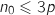 .
.
Pour tout entier 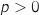 :
:
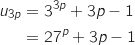 Comme
Comme 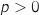 ,
, 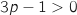 et du coup on a
et du coup on a 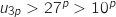 .
Comme
.
Comme  est croissante pour tout entier
est croissante pour tout entier 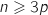 , on a
, on a 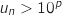 , donc le plus petit entier
, donc le plus petit entier 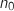 qui permette de réaliser la condition sera tel que
qui permette de réaliser la condition sera tel que 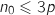 .
.
c. Déterminer à l'aide de la calculatrice cet entier 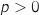 :
:
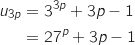 Comme
Comme 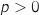 ,
, 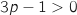 et du coup on a
et du coup on a 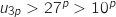 .
Comme
.
Comme  est croissante pour tout entier
est croissante pour tout entier 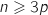 , on a
, on a 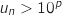 , donc le plus petit entier
, donc le plus petit entier 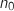 qui permette de réaliser la condition sera tel que
qui permette de réaliser la condition sera tel que 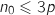 .
.
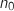 pour la valeur
pour la valeur 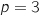 .
.
On a 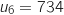 et
et 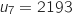 , donc pour
, donc pour 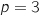 ,
, 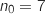 .
.
d. Proposer un algorithme qui, pour une valeur de 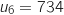 et
et 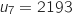 , donc pour
, donc pour 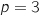 ,
, 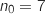 .
.
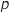 donnée en entrée, affiche en sortie la valeur du plus petit entier
donnée en entrée, affiche en sortie la valeur du plus petit entier 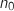 tel que, pour tout
tel que, pour tout 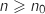 , on ait
, on ait 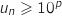 .
.
Variables
U est un réel
p est un entier
n est un entier
Initialisation
U:= 0
n:= 0
Entrée
Saisir p (entier strictement positif)
Traitement
Tant que U<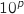 faire
n:= n+1
U:= 3
faire
n:= n+1
U:= 3 +n-1
Fin tant que
Sortie
Afficher n.
+n-1
Fin tant que
Sortie
Afficher n.
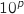 faire
n:= n+1
U:= 3
faire
n:= n+1
U:= 3 +n-1
Fin tant que
Sortie
Afficher n.
+n-1
Fin tant que
Sortie
Afficher n.
