Corrigé de l'exercice 4 du bac S de maths de juin 2012 en Polynésie
Cacher les corrigés
On désigne par un réel appartenant à l'intervalle
un réel appartenant à l'intervalle 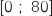 .
Une urne contient 100 petits cubes en bois dont 60 sont bleus et les autres rouges.
Parmi les cubes bleus, 40% ont leurs faces marquées d'un cercle, 20 % ont leur faces marquées d'un losange et les autres ont leurs faces marquées d'une étoile.
Parmi les cubes rouges, 20% ont leurs faces marquées d'un cercle
.
Une urne contient 100 petits cubes en bois dont 60 sont bleus et les autres rouges.
Parmi les cubes bleus, 40% ont leurs faces marquées d'un cercle, 20 % ont leur faces marquées d'un losange et les autres ont leurs faces marquées d'une étoile.
Parmi les cubes rouges, 20% ont leurs faces marquées d'un cercle  % ont leurs faces marquées d'un losange et les autres ont leurs faces marquées d'une étoile.
% ont leurs faces marquées d'un losange et les autres ont leurs faces marquées d'une étoile.
Partie A : Expérience 1
On tire au hasard un cube de l'urne. 1. Démontrer que la probabilité que soit tiré un cube marqué d'un losange est égale à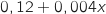 .
.
Pour y voir plus clair on défini les événements suivants :
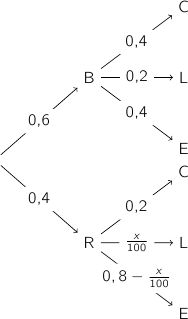
Les événements B et R consituent un système complet d'événements donc d'après la formule des probabilités totales :
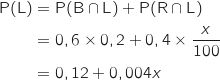
- R : « le cube tiré est rouge »,
- B : « le cube tiré est bleu »,
- C : « le cube tiré est marqué d'un cercle »,
- L : « le cube tiré est marqué d'un losange »,
- E : « le cube tiré est marqué d'une étoile ».

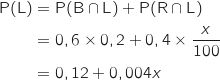
2. Déterminer
 pour que la probabilité de tirer un cube marqué d'un losange soit égale à celle de tirer un cube marqué d'une étoile.
pour que la probabilité de tirer un cube marqué d'un losange soit égale à celle de tirer un cube marqué d'une étoile.
En utilisant comme dans la question précédente la formule des probabilités totales on a :
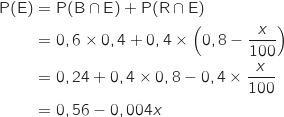 Il s'agit maintenant de résoudre :
Il s'agit maintenant de résoudre :
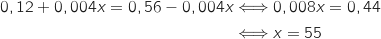 Donc pour avoir
Donc pour avoir 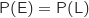 , il faut que 55% des cubes rouges soient marqués avec un losange.
, il faut que 55% des cubes rouges soient marqués avec un losange.
3. Déterminer 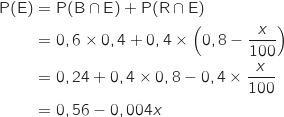 Il s'agit maintenant de résoudre :
Il s'agit maintenant de résoudre :
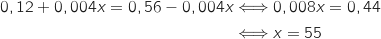 Donc pour avoir
Donc pour avoir 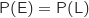 , il faut que 55% des cubes rouges soient marqués avec un losange.
, il faut que 55% des cubes rouges soient marqués avec un losange.
 pour que les événements « tirer un cube bleu » et « tirer un cube marqué d'un losange » soient indépendants.
pour que les événements « tirer un cube bleu » et « tirer un cube marqué d'un losange » soient indépendants.
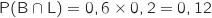
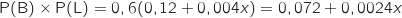 .
L'indépendance équivaut à
.
L'indépendance équivaut à 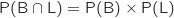 soit :
soit :
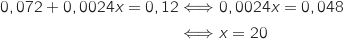 Donc pour avoir l'indépendance entre les événements B et L il faut que 20% des cubes rouges soient marqués avec un losange.
Donc pour avoir l'indépendance entre les événements B et L il faut que 20% des cubes rouges soient marqués avec un losange.
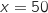 .
Calculer la probabilité que soit tiré un cube bleu sachant qu'il est marqué d'un losange.
.
Calculer la probabilité que soit tiré un cube bleu sachant qu'il est marqué d'un losange.
Pour 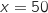 on a
on a 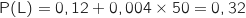 .
En utilisant la formule des probabilités conditionnelles :
.
En utilisant la formule des probabilités conditionnelles :
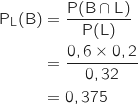
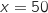 on a
on a 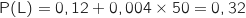 .
En utilisant la formule des probabilités conditionnelles :
.
En utilisant la formule des probabilités conditionnelles :
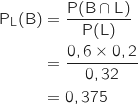
La deuxième partie du sujet utilise des notions de dénombrement qui ne sont plus au programme à partir de la
session 2013 du baccalauréat.
