Sujet et corrigé de l'exercice 3 du bac S de maths de juin 2013 en Polynésie
Cacher les corrigés
Thomas possède un lecteur MP3 sur lequel il a stocké plusieurs milliers de morceaux musicaux. L'ensemble des morceaux musicaux qu'il possède se divise en trois genres distincts selon la répartition suivante :- Les
 des morceaux de musique classique sont encodés en haute qualité,
des morceaux de musique classique sont encodés en haute qualité,
- Les
 des morceaux de variété sont encodés en qualité standard.
des morceaux de variété sont encodés en qualité standard.
On considérera les événements suivants : C : « Le morceau écouté est un morceau de musique classique » ; V : « Le morceau écouté est un morceau de variété » ; J : « Le morceau écouté est un morceau de jazz » ; H : « Le morceau écouté est encodé en haute qualité » ; S : « Le morceau écouté est encodé en qualité standard ».
Partie 1
Thomas décide d'écouter un morceau au hasard parmi tous les morceaux stockés sur son MP3 en utilisant la fonction « lecture aléatoire ». On pourra s'aider d'un arbre de probabilités. 1. Quelle est la probabilité qu'il s'agisse d'un morceau de musique classique encodé en haute qualité ?
 .
.
2. On sait que
 .
a. Les événements C et H sont-ils indépendants ?
.
a. Les événements C et H sont-ils indépendants ?
Pour savoir si C et H sont indépendants on compare  avec
avec  .
Ainsi
.
Ainsi  , donc les événements C et H ne sont pas indépendants.
, donc les événements C et H ne sont pas indépendants.
b. Calculer  avec
avec  .
Ainsi
.
Ainsi  , donc les événements C et H ne sont pas indépendants.
, donc les événements C et H ne sont pas indépendants.
 et
et  .
.
Les événements C, V et J forment une partition de l'univers donc la formule des probabilités totales donne :
 En remplaçant par les données connues il vient :
En remplaçant par les données connues il vient :
 D'où
D'où  Enfin pour terminer :
Enfin pour terminer :  .
.
 En remplaçant par les données connues il vient :
En remplaçant par les données connues il vient :
 D'où
D'où  Enfin pour terminer :
Enfin pour terminer :  .
.
Partie 2
Pendant un long trajet en train, Thomas écoute, en utilisant la fonction « lecture aléatoire » de son MP3, 60 morceaux de musique. 1. Déterminer l'intervalle de fluctuation asymptotique au seuil de 95 % de la proportion de morceaux de musique classique dans un échantillon de taille 60.
On utilise directement l'intervalle vu en cours :

 et
et  .
On peut remarquer que les conditions usuelles d'utilisation sont vérifiées :
.
On peut remarquer que les conditions usuelles d'utilisation sont vérifiées :
 et
et 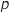 par leurs valeurs l'intervalle obtenu est :
par leurs valeurs l'intervalle obtenu est :

2. Thomas a comptabilisé qu'il avait écouté 12 morceaux de musique classique pendant son voyage. Peut-on penser
que la fonction « lecture aléatoire » du lecteur MP3 de Thomas est défectueuse ?

 et
et  .
On peut remarquer que les conditions usuelles d'utilisation sont vérifiées :
.
On peut remarquer que les conditions usuelles d'utilisation sont vérifiées :
-
 , donc
, donc 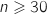
-
 , donc
, donc 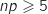
-
 , donc
, donc 
 et
et 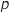 par leurs valeurs l'intervalle obtenu est :
par leurs valeurs l'intervalle obtenu est :

La proportion de morceaux de musique classique observée sur l'échantillon de Thomas est  .
.
 , donc on ne peut pas penser que la fonction « lecture aléatoire » du lecteur est défectueuse.
, donc on ne peut pas penser que la fonction « lecture aléatoire » du lecteur est défectueuse.
 .
.
 , donc on ne peut pas penser que la fonction « lecture aléatoire » du lecteur est défectueuse.
, donc on ne peut pas penser que la fonction « lecture aléatoire » du lecteur est défectueuse.
Partie 3
On considère la variable aléatoire qui, à chaque chanson stockée sur le lecteur MP3, associe sa durée
exprimée en secondes et on établit que
qui, à chaque chanson stockée sur le lecteur MP3, associe sa durée
exprimée en secondes et on établit que  suit la loi normale d'espérance 200 et d'écart-type 20.
On pourra utiliser le tableau fourni ci-dessous dans lequel les valeurs sont arrondies au millième le plus proche.
suit la loi normale d'espérance 200 et d'écart-type 20.
On pourra utiliser le tableau fourni ci-dessous dans lequel les valeurs sont arrondies au millième le plus proche.

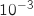 près de
près de  .
.
 .
.
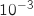 près de la probabilité que le morceau écouté dure plus de 4 minutes.
près de la probabilité que le morceau écouté dure plus de 4 minutes.
4 minutes correspondent à 240 secondes dont on calcule :
 .
.
 .
.
