Sujet et corrigé de l'exercice 4 du bac S de maths de juin 2013 en Polynésie
Cacher les corrigés
On considère la suite
définie par 
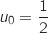et telle que pour tout entier naturel 
,
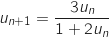
1.a. Calculer
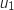et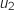 
.
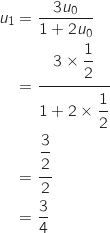
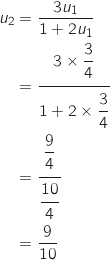
b. Démontrer, par récurrence, que pour tout entier naturel
, 
.
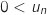Initilisation au rang 0
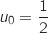; donc on a bien 
.
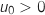Hérédité
On suppose que la propriété est vraie à un rang 
, c'est à dire qu'on suppose que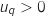 
.
D'une part,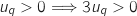 
;
d'autre part,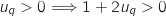 
.
Donc le quotient 
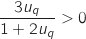, soit 
.
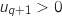Ainsi la propriété est également vraie au rang 
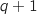ce qui montre l'hérédité.
La propriété étant vraie au rang 0 et étant héréditaire, elle est vraie pour tout entier naturel .
2. On admet que, pour tout entier naturel 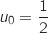; donc on a bien .
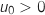Hérédité
On suppose que la propriété est vraie à un rang , c'est à dire qu'on suppose que .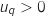
D'une part, ;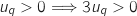
d'autre part, .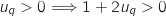
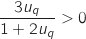Donc le quotient , soit .
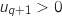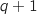Ainsi la propriété est également vraie au rang ce qui montre l'hérédité.
La propriété étant vraie au rang 0 et étant héréditaire, elle est vraie pour tout entier naturel .
, 
.
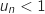a. Démontrer que la suite est croissante.
Pour tout entier naturel :
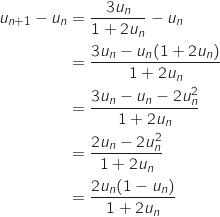On sait que 
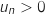, donc 
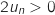et 
;
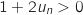on sait que 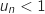, donc 
.
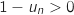Tous les facteurs du quotient sont strictement positifs, donc le quotient aussi et il s'ensuit que la suite est strictement croissante.
b. Démontrer que la suite :
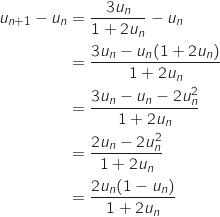On sait que 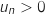, donc 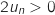et ;
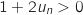on sait que 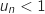, donc .
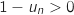Tous les facteurs du quotient sont strictement positifs, donc le quotient aussi et il s'ensuit que la suite est strictement croissante.
converge.
La suite est croissante et majorée par 1 donc elle est convergente (théorème de convergence monotone).
3. Soit est croissante et majorée par 1 donc elle est convergente (théorème de convergence monotone).
la suite définie, pour tout entier naturel , par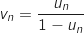 
.
a. Montrer que la suite est une suite géométrique de raison 3.
Pour tout entier naturel :
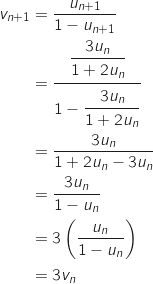Donc la suite est bien une suite géométrique de raison 3.
b. Exprimer pour tout entier naturel :
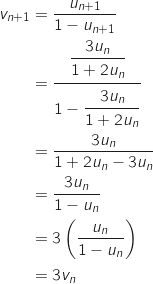Donc la suite est bien une suite géométrique de raison 3.
, 
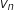en fonction de .
Le premier terme de la suite géométrique mise en évidence dans la question précédente est :
.
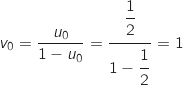Donc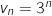 
.
c. En déduire que, pour tout entier naturel .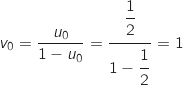
Donc .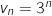
, 
.
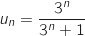Pour tout entier naturel on a :
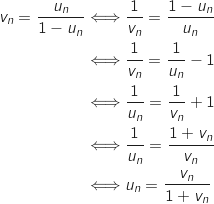En remplaçant 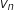par sa formule explicite il vient :
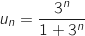
d. Déterminer la limite de la suite on a :
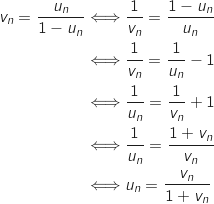En remplaçant 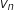par sa formule explicite il vient :
.
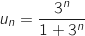
On a une forme indéterminée mais on peut écrire :
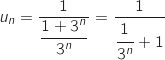
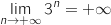car 
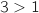; par inverse : 
.
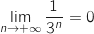Donc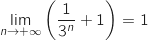 
et en inversant, 
.
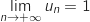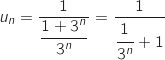
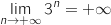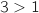car ; par inverse : .
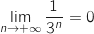Donc 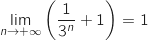et en inversant, .
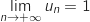