Sujet et corrigé de l'exercice de spécialité du bac S de maths de juin 2013 en Polynésie
Cacher les corrigés
Un opérateur téléphonique A souhaite prévoir l'évolution du nombre de ses abonnés dans une grande ville par rapport à son principal concurrent B à partir de 2013. En 2013, les opérateurs A et B ont chacun 300 milliers d'abonnés. Pour tout entier naturel , on note
, on note 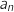 le nombre d'abonnés, en milliers, de l'opérateur A la
le nombre d'abonnés, en milliers, de l'opérateur A la  -ième année après 2013,
et
-ième année après 2013,
et 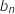 le nombre d'abonnés, en milliers, de l'opérateur B la
le nombre d'abonnés, en milliers, de l'opérateur B la  -ième année après 2013.
Ainsi,
-ième année après 2013.
Ainsi, 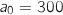 et
et 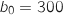 .
.
Des observations réalisées les années précédentes conduisent à modéliser la situation par la relation suivante : pour tout entier naturel
 ,
,
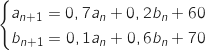 .
On considère les matrices
.
On considère les matrices 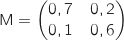 et
et 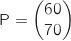 .
Pour tout entier naturel
.
Pour tout entier naturel  , on note
, on note 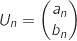 .
1.a. Déterminer
.
1.a. Déterminer 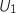 .
.
En utilisant la relation fournie on obtient :
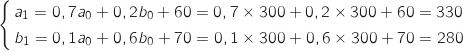
b. Vérifier que, pour tout entier naturel 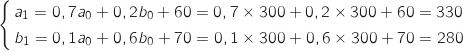
 ,
, 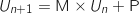 .
.
On calcule déjà :
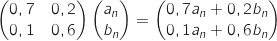 En ajoutant P, on obtient :
En ajoutant P, on obtient :
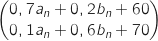 ,
ce qui correspond bien à
,
ce qui correspond bien à 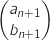
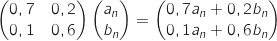 En ajoutant P, on obtient :
En ajoutant P, on obtient :
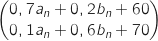 ,
ce qui correspond bien à
,
ce qui correspond bien à 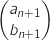
2. On note I la matrice
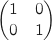 .
a. Calculer
.
a. Calculer 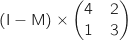 .
.
On a déjà : 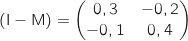 Puis :
Puis : 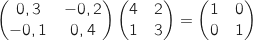
b. En déduire que la matrice 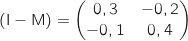 Puis :
Puis : 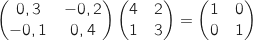
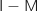 est inversible et préciser son inverse.
est inversible et préciser son inverse.
D'après le calcul précédent la matrice 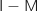 est inversible et son inverse
est
est inversible et son inverse
est 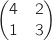 .
.
c. Déterminer la matrice U telle que 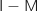 est inversible et son inverse
est
est inversible et son inverse
est 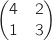 .
.
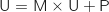 .
.
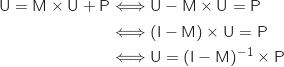 En utilisant l'inverse de
En utilisant l'inverse de 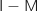 vue ci-avant on obtient :
vue ci-avant on obtient :
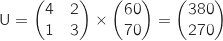
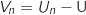 .
a. Justifier que, pour tout entier naturel
.
a. Justifier que, pour tout entier naturel  ,
, 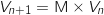 .
.
Pour tout entier naturel  on a :
on a :
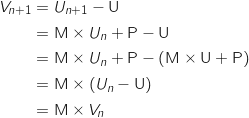
b. En déduire que, pour tout entier naturel  on a :
on a :
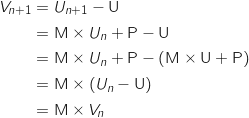
 ,
, 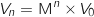 .
.
On peut faire une démonstration par récurrence de la propriété :  :
«
:
« 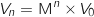 ».
Initialisation au rang 0
».
Initialisation au rang 0
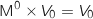 , donc la propriété est vraie au rang 0.
Hérédité
On suppose qu'à un rang q on a :
, donc la propriété est vraie au rang 0.
Hérédité
On suppose qu'à un rang q on a : 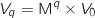 On a alors :
On a alors :
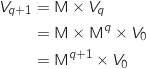 Donc la propriété est vraie au rang
Donc la propriété est vraie au rang 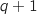 , ce qui prouve l'hérédité.
La propriété est vraie au rang 0, elle est héréditaire, donc elle vraie pour tout entier
naturel.
, ce qui prouve l'hérédité.
La propriété est vraie au rang 0, elle est héréditaire, donc elle vraie pour tout entier
naturel.
4. On admet que, pour tout entier naturel  :
«
:
« 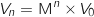 ».
Initialisation au rang 0
».
Initialisation au rang 0
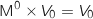 , donc la propriété est vraie au rang 0.
Hérédité
On suppose qu'à un rang q on a :
, donc la propriété est vraie au rang 0.
Hérédité
On suppose qu'à un rang q on a : 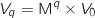 On a alors :
On a alors :
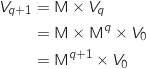 Donc la propriété est vraie au rang
Donc la propriété est vraie au rang 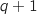 , ce qui prouve l'hérédité.
La propriété est vraie au rang 0, elle est héréditaire, donc elle vraie pour tout entier
naturel.
, ce qui prouve l'hérédité.
La propriété est vraie au rang 0, elle est héréditaire, donc elle vraie pour tout entier
naturel.
 ,
,
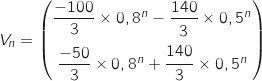
 , exprimer
, exprimer 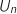 en fonction de
en fonction de  et en déduire la limite de la suite
et en déduire la limite de la suite 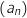 .
.
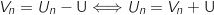 , du coup on obtient :
, du coup on obtient :
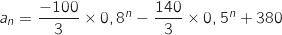 Comme
Comme 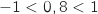 et
et 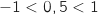 ,
,
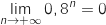 et
et
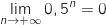 .
et
.
et 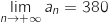 ,
,
D'après ce qui précéde, à long terme, le nombre d'abonnés de l'opérateur A va se stabiliser
autour de 380 milliers d'abonnés.
