Sujet et corrigé de l'exercice 2 du bac S de maths de juin 2014 en Polynésie
Cacher les corrigés
On considère la suite définie par
et, pour tout entier naturel ,
1. Calculer et .
2. On considère les deux algorithmes suivants :
Algorithme 1 :
| Variables : | est un entier naturel |
| est un réel | |
| Entrée : | Saisir la valeur de |
| Traitement : | prend la valeur 0 |
| Pour allant de 1 à faire | |
| prend la valeur | |
| Fin Pour | |
| Sortie : | Afficher |
Algorithme 2 :
| Variables : | est un entier naturel |
| est un réel | |
| Entrée : | Saisir la valeur de |
| Traitement : | prend la valeur 0 |
| Pour allant de 0 à faire | |
| prend la valeur | |
| Fin Pour | |
| Sortie : | Afficher |
De ces deux algorithmes, lequel permet d'afficher en sortie la valeur de , la valeur de l'entier naturel étant entrée par l'utilisateur ?
Dans la boucle de calcul, la valeur de doit correspondre à l'indice du terme précédent celui qui est en train d'être calculé.
Dans l'algorithme 1, il n'y a pas ce « décalage », par exemple au premier passage on calcule et la valeur de est 1 du coup on calcule :
, alors qu'il faut calculer .
Par contre dans l'algorithme 2, c'est bon.
3. A l'aide de l'algorithme, on a obtenu le tableau et le nuage de points ci-dessous où figure en abscisse et en ordonnée.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 0 | 2 | 6 | 12 | 20 | 30 | 42 | 56 | 72 | 90 | 110 | 132 | 156 |
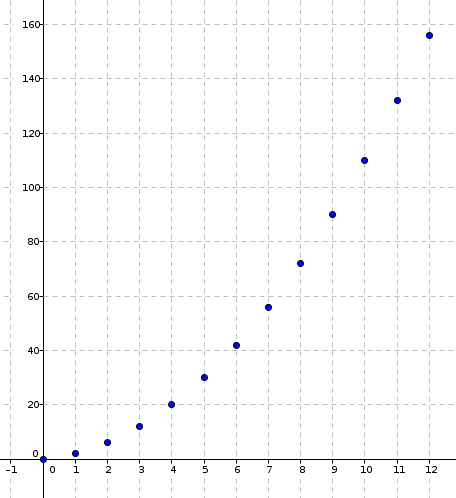
a. Quelle conjecture peut-on faire quant au sens de variation de la suite ?
Démontrer cette conjecture.
On conjecture que la suite est croissante.
Pour tout entier naturel :
donc
Comme , on en conclut que et donc que la suite est strictement croissante.
b. La forme parabolique du nuage de points amène à conjecturer l'existence de trois réels et tels que, pour tout entier naturel :
Dans le cadre de cette conjecture, trouver les valeurs de et à l'aide des informations fournies.
Comme il y a trois inconnue on forme un système de 3 équations, en utilisant, par exemple, les valeurs de , et , ce qui donne :
Donc .
4. On définit, pour tout entier naturel , la suite par :
a. Exprimer en fonction de l'entier naturel .
Quelle est la nature de la suite ?
Pour tout entier naturel :
On reconnaît la formule explicite d'une suite arithmétique de premier terme 2 et de raison 2.
On définit, pour tout entier naturel :
Démontrer que, pour tout entier naturel , .
La somme des premiers termes de la suite arithmétique vaut :
c. Démontrer que, pour tout entier naturel , , puis exprimer en fonction de .
Pour tout entier naturel :
On obtient le résultat final en enlevant tous les termes qui s'annulent.
Donc on a .
Comme par ailleurs il vient :
En posant , on aboutit à :
,
on retrouve la formule explicite trouvée dans la question 3.b.
