Sujet et corrigé de l'exercice 4 du bac S de maths de juin 2014 en Polynésie
Cacher les corrigés
Soient et les fonctions définies sur par
On note et les courbes représentatives des fonctions et dans un repère orthogonal.
1. Démontrer que les courbes et ont un point commun d'abscisse et qu'en ce point, elles ont la même tangente dont on déterminera une équation.
Donc et ont en commun le point .
Pour déterminer les équations des tangentes on calcule les dérivées :
et
et
Comme et , les courbes ont la même tangente en dont une équation est :
soit .
2. Etude de la position relative de la courbe et de la droite .
Soit la fonction définie sur par
a. Déterminer la limite de la fonction en .
, donc par composée
Finalement par somme : .
b. Justifier que, pour tout réel ,
En déduire la limite de la fonction en .
Pour tout réel :
,
(limite connue),
donc par composition : ;
Donc par somme :
En multipliant par qui tend également vers on a finalement :
c. On note la fonction dérivée de la fonction sur .
Pour tout réel , calculer et étudier le signe de suivant les valeurs de .
La fonction est dérivable sur et on a :
On résout, par exemple :
Donc .
De même on a :
d. Dresser le tableau de variations de la fonction sur .
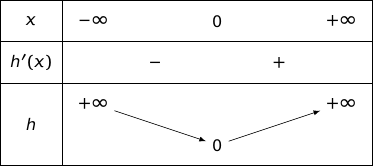
e. En déduire que, pour tout réel , .
D'après l'étude précédente, pour tout , , soit :
f. Que peut-on en déduire quant à la position relative de la courbe et de la droite ?
L'inégalité précédente correspond à
où l'équation réduite de est .
Cela signifie que la courbe est située au dessus de .
3. Etude de la position relative des courbes et
a. Pour tout réel , développer l'expression .
Pour tout nombre réel on a :
b. Déterminer la position relative des courbes et .
Pour tout réel :
Donc pour tout nombre réel :
, soit ,
cela montre que est au dessus de .
4. Calculer, en unité d'aire, l'aire du domaine compris entre les courbes et et les droites d'équations respectives et .
Compte tenu de la position de par rapport à , l'aire du domaine demandé se calcule par :
