Corrigé de l'exercice 1 du bac S de maths 2012 à Pondichéry
Cacher les corrigés
Partie A
Un groupe de 50 coureurs, portant des dossards numérotés de 1 à 50, participe à une course cycliste qui comprend 10 étapes, et au cours de laquelle aucun abandon n'est constaté. A la fin de chaque étape, un groupe de 5 coureurs est choisi au hasard pour subir un contrôle antidopage. Ces désignations de 5 coureurs à l'issue de chacune des étapes sont indépendantes. Un même coureur peut donc être contrôlé à l'issue de plusieurs étapes.
Dans le sujet original certaines questions nécessitent l'utilisation de notions de combinatoire qui ne figurent plus
au programme à partir de la rentrée 2012. Ces questions ont été supprimées.
2. On considère l'algorithme ci-dessous dans lequel :
- « rand(1,50) » permet d'obtenir un nombre entier aléatoire appartenant à l'intervalle [1;50]
- l'écriture «
» désigne l'affectation d'une valeur 
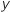à une variable 
.
?
La boucle tant que est réitérée tant qu'il y a au moins deux nombres parmi 
qui sont égaux, ce qui assure que les nombres affichés à la fin de l'algorihme sont tous distincts.
Donc seules les listes 
et 
ont pu être obtenues avec cet algorihtme (listes ne comportant pas de doublon).
b. Que permet de réaliser cet algorithme concernant la course cycliste ?
qui sont égaux, ce qui assure que les nombres affichés à la fin de l'algorihme sont tous distincts.
Donc seules les listes et ont pu être obtenues avec cet algorihtme (listes ne comportant pas de doublon).
Cet algorithme permet de tirer au sort 5 numéros de dossards distincts pour désigner les 5 coureurs qui subiront le contrôle anti-dopage à l'issue d'une étape.
3. A l'issue d'une étape, on choisit au hasard un coureur parmi les 50 participants. On admet que la probabilité pour qu'il subisse le contrôle prévu pour cette étape est égale à 0,1. 4. On note la variable aléatoire qui comptabilise le nombre de contrôles subis par un coureur sur l'ensemble des 10 étapes de la course. a. Quelle est la loi de probabilité de la variable aléatoire
? Préciser ses paramètres.
On repète de manière indépendante 10 fois l'expérience de Bernoulli qui consiste à choisir ou non le coureur pour le contrôler, la probabilité qu'il soit choisi étant 0,1, donc la variable aléatoire
qui compte le nombre de fois où il a été choisi suit une loi binomiale 
.
b. On choisit au hasard un coureur à l'arrivée de la course. Calculer, sous forme décimale
arrondie au dix-millième, les probabilités des événements suivants :
qui compte le nombre de fois où il a été choisi suit une loi binomiale .
- il a été contrôlé 5 fois exactement ;
- il n'a pas eté contrôlé ;
- il a eté contrôlé au moins une fois.
En utilisant la variable aléatoire de la question précédente on a :
de la question précédente on a :
-
-
-
.
Partie B
Dans cette partie, toute trace de recherche même incomplète, ou d'initiative même non fructueuse, sera prise en compte dans l évaluation. On donnera les résultats sous forme de fraction irréductible. Pour un coureur choisi au hasard dans l'ensemble des 50 coureurs, on appelle T l'événement « le contrôle est positif », et d'après des statistiques, on admet que
.
On appelle D l'événement : « le coureur est dopé ».
Le contrôle anti-dopage n'étant pas fiable à 100 %, on sait que :
- si un coureur est dopé, le contrôle est positif dans 97 % des cas ;
- si un coureur n'est pas dopé, le contrôle est positif dans 1% des cas.
.
On peut représenter la situation sous forme d'un arbre en notant 
:
Les événements D et 
constituent un système complet d'événements donc en utilisant la formule des probabilités totales on a :
Comme on sait que , on obtient l'équation :
.
2. Un coureur a un contrôle positif. Quelle est la probabilité qu'il ne soit pas dopé ?
:
constituent un système complet d'événements donc en utilisant la formule des probabilités totales on a :
Comme on sait que , on obtient l'équation :
.
On calcule : 
.
.
