Corrigé de l'exercice 3 du bac S 2012 de maths du bac à Pondichéry
Cacher les corrigés
On considère les suites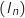 et
et 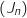 définies pour tout entier naturel
définies pour tout entier naturel  par :
par :

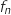 définies sur l'intervalle
définies sur l'intervalle  par
par
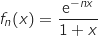
 :
:
a. Formuler une conjecture sur le sens de variation de la suite
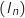 en expliquant la démarche.
en expliquant la démarche.
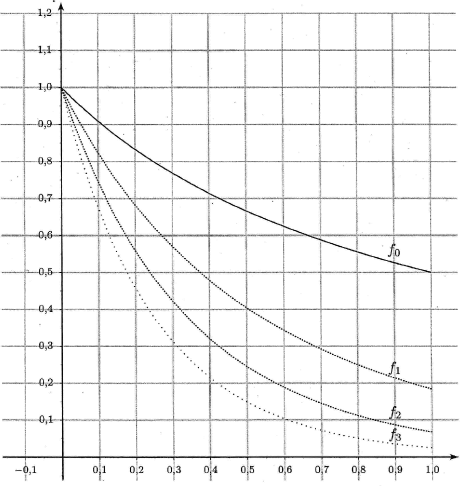
Sur l'intervalle  , les fonctions
, les fonctions 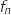 sont définies, continues et positives. Donc pour
tout entier naturel
sont définies, continues et positives. Donc pour
tout entier naturel  ,
, 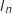 représente l'aire du domaine délimité par la courbe représentative de
représente l'aire du domaine délimité par la courbe représentative de 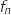 , l'axe des abscisses, la droite d'équation
, l'axe des abscisses, la droite d'équation 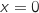 et
la droite d'équation
et
la droite d'équation  .
Par observation du graphique, l'aire de ce domaine diminue lorsque
.
Par observation du graphique, l'aire de ce domaine diminue lorsque  augmente, ainsi on conjecture que la suite
augmente, ainsi on conjecture que la suite 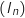 est décroissante.
est décroissante.
b. Démontrer cette conjecture.
 , les fonctions
, les fonctions 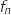 sont définies, continues et positives. Donc pour
tout entier naturel
sont définies, continues et positives. Donc pour
tout entier naturel  ,
, 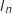 représente l'aire du domaine délimité par la courbe représentative de
représente l'aire du domaine délimité par la courbe représentative de 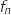 , l'axe des abscisses, la droite d'équation
, l'axe des abscisses, la droite d'équation 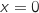 et
la droite d'équation
et
la droite d'équation  .
Par observation du graphique, l'aire de ce domaine diminue lorsque
.
Par observation du graphique, l'aire de ce domaine diminue lorsque  augmente, ainsi on conjecture que la suite
augmente, ainsi on conjecture que la suite 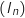 est décroissante.
est décroissante.
Pour tout entier naturel  , on a :
, on a :
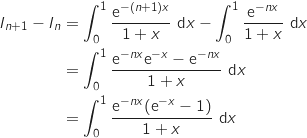 Pour tout
Pour tout 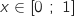 , le signe de
, le signe de 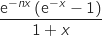 est le même que celui de
est le même que celui de 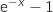 .
.
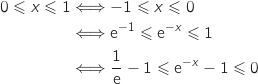 Donc pour tout
Donc pour tout 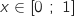 ,
, 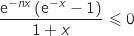 et donc
et donc 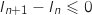 soit
soit
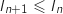 ce qui prouve que la suite
ce qui prouve que la suite 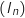 est décroissante.
est décroissante.
 , on a :
, on a :
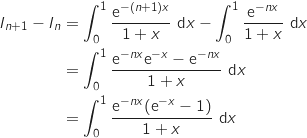 Pour tout
Pour tout 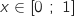 , le signe de
, le signe de 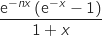 est le même que celui de
est le même que celui de 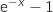 .
.
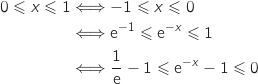 Donc pour tout
Donc pour tout 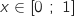 ,
, 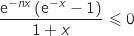 et donc
et donc 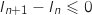 soit
soit
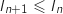 ce qui prouve que la suite
ce qui prouve que la suite 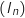 est décroissante.
est décroissante.
2.a. Montrer que pour tout entier
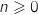 et pour tout nombre réel
et pour tout nombre réel  de l'intervalle
de l'intervalle  :
:
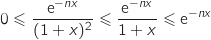
Pour tout entier 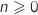 et pour tout
et pour tout 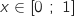 , les quantités qui interviennent sont de façon évidente positives.
, les quantités qui interviennent sont de façon évidente positives.
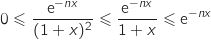
b. Montrer que les suites 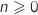 et pour tout
et pour tout 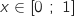 , les quantités qui interviennent sont de façon évidente positives.
, les quantités qui interviennent sont de façon évidente positives.
- Comparaison de
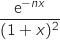 et
et 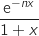 :
:
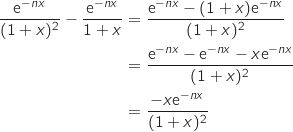 Comme
Comme 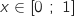 , cette dernière quantité est négative donc on a :
, cette dernière quantité est négative donc on a :
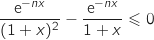 , soit
, soit
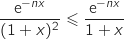
- Comparaison de
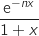 et
et 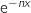
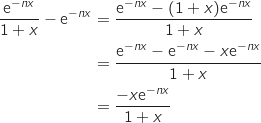 Comme précédemment la quantité obtenue est négative pour
Comme précédemment la quantité obtenue est négative pour 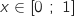 donc :
donc :
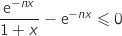 soit
soit 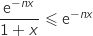 .
.
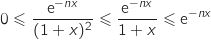
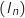 et
et 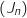 sont convergentes et déterminer leur limite.
sont convergentes et déterminer leur limite.
On intègre sur  l'inégalité précédente (on rappelle que l'intégration conserve l'ordre à condition que la borne inférieure de l'intégrale, ici 0, soit
inférieure à la borne supérieure, ici 1) :
l'inégalité précédente (on rappelle que l'intégration conserve l'ordre à condition que la borne inférieure de l'intégrale, ici 0, soit
inférieure à la borne supérieure, ici 1) :
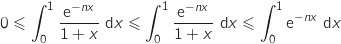
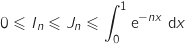 .
Il reste à calculer :
.
Il reste à calculer :
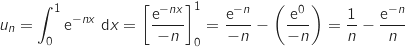 .
On a :
.
On a :
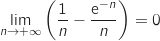 .
Ainsi on a :
.
Ainsi on a : 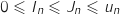 avec
avec 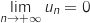 , donc d'après le théorème des gendarmes les suite
, donc d'après le théorème des gendarmes les suite 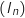 et
et 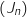 convergent vers 0.
convergent vers 0.
3.a. On admet que pour tout entier  l'inégalité précédente (on rappelle que l'intégration conserve l'ordre à condition que la borne inférieure de l'intégrale, ici 0, soit
inférieure à la borne supérieure, ici 1) :
l'inégalité précédente (on rappelle que l'intégration conserve l'ordre à condition que la borne inférieure de l'intégrale, ici 0, soit
inférieure à la borne supérieure, ici 1) :
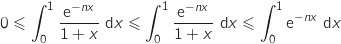
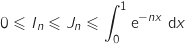 .
Il reste à calculer :
.
Il reste à calculer :
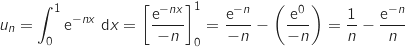 .
On a :
.
On a :
-
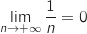
-
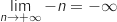 et par composition
et par composition 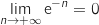 , enfin
par quotient
, enfin
par quotient 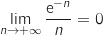
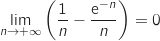 .
Ainsi on a :
.
Ainsi on a : 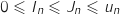 avec
avec 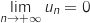 , donc d'après le théorème des gendarmes les suite
, donc d'après le théorème des gendarmes les suite 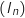 et
et 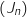 convergent vers 0.
convergent vers 0.
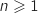 :
:
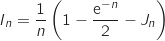
Dans le sujet original il faut établir la relation proposée en effectuant une intégration par parties.
Depuis la rentrée 2012, la méthode d'intégration par parties ne figure plus dans les programmes.
b. En déduire 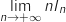 .
.
En utilisant la relation précédente :
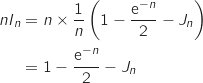 On a :
On a : 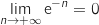 et
et 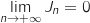 donc par somme
donc par somme
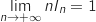 .
.
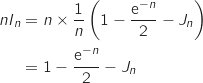 On a :
On a : 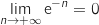 et
et 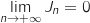 donc par somme
donc par somme
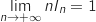 .
.
