Corrigé de l'exercice 4 du bac S 2012 de maths à Pondichéry
Cacher les corrigés
Partie A : Restitution organisée de connaissances
Soit un nombre complexe. On rappelle que
un nombre complexe. On rappelle que 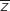 est le conjugué de
est le conjugué de  et que
et que 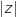 est le module de
est le module de  .
On admet l'égalité :
.
On admet l'égalité : 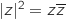 .
Montrer que, si
.
Montrer que, si 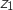 et
et 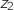 sont deux nombres complexes, alors
sont deux nombres complexes, alors 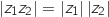 .
.
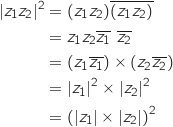 On a donc l'égalité entre carrés :
On a donc l'égalité entre carrés : 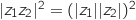 et comme les modules sont positifs on en déduit que
et comme les modules sont positifs on en déduit que 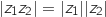 .
.
Partie B : Etude d'une transformation particulière
Dans le plan complexe rapporté au repère orthonormal direct , on désigne par A et B les points d'affixes respectives
, on désigne par A et B les points d'affixes respectives 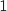 et
et 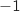 .
Soit
.
Soit  la transformation du plan qui à tout point
la transformation du plan qui à tout point 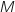 d'affixe
d'affixe 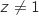 , associe le point
, associe le point 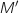 d'affixe
d'affixe 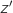 tel que:
tel que:
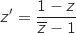
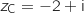 .
a. Calculer l'affixe
.
a. Calculer l'affixe 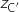 du point C' image de C par la transformation
du point C' image de C par la transformation  , et placer les points C et C'.
, et placer les points C et C'.
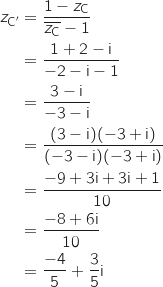
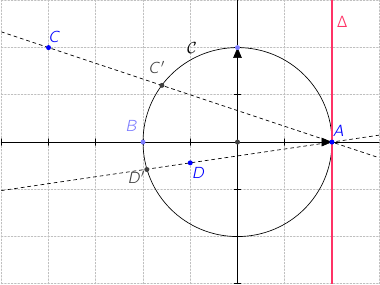
b. Montrer que le point C' appartient au cercle
 de centre O et de rayon 1.
de centre O et de rayon 1.
On a 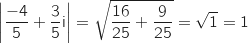 Donc C'
Donc C'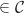 .
.
c. Montrer que les points A, C et C' sont alignés.
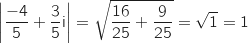 Donc C'
Donc C'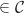 .
.
On a :
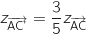 donc les vecteurs
donc les vecteurs 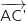 et
et 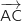 sont colinéaires
ce qui prouve que A, C et C' sont alignés.
sont colinéaires
ce qui prouve que A, C et C' sont alignés.
2. Déterminer et représenter sur la figure l'ensemble -
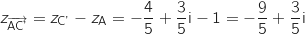 .
.
-
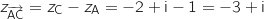
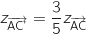 donc les vecteurs
donc les vecteurs 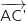 et
et 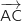 sont colinéaires
ce qui prouve que A, C et C' sont alignés.
sont colinéaires
ce qui prouve que A, C et C' sont alignés.
 des points du plan qui ont le point A pour image par la transformation
des points du plan qui ont le point A pour image par la transformation  .
.
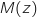 avec
avec 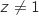 , a pour image A par
, a pour image A par  équivaut à :
équivaut à :
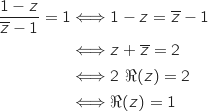 Donc l'ensemble cherché est constitué des points de la droite d'équation
Donc l'ensemble cherché est constitué des points de la droite d'équation  privée de A (on n'oublie pas que
privée de A (on n'oublie pas que 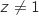 ).
).
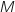 distinct de A, le point
distinct de A, le point 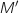 appartient au cercle
appartient au cercle  .
.
On a pour tout 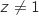 :
:
 Donc
Donc 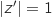 , ce qui justifie que
, ce qui justifie que 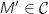 .
.
4. Montrer que, pour tout nombre complexe 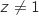 :
:
 Donc
Donc 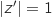 , ce qui justifie que
, ce qui justifie que 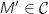 .
.
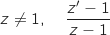 est réel.
Que peut-on en déduire pour les points A,
est réel.
Que peut-on en déduire pour les points A, 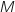 et
et 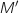 ?
?
Pour 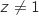 , on a :
, on a :
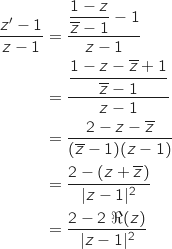 On obtient un résultat qui ne contient que des nombres réels donc
On obtient un résultat qui ne contient que des nombres réels donc 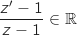 .
Pour
.
Pour 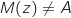 et
et 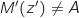 , on remarque que
, on remarque que 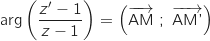 , or
, or
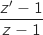 est réel, dont un argument est 0 ou
est réel, dont un argument est 0 ou 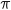 , soit
, soit 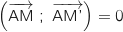 ou
ou 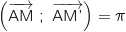 ce qui justifie que A,
ce qui justifie que A, 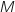 et
et 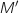 sont alignés.
sont alignés.
5. On a placé un point D sur la figure. Construire son image D' par la transformation 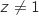 , on a :
, on a :
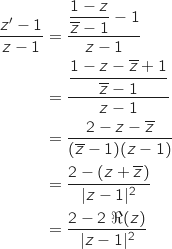 On obtient un résultat qui ne contient que des nombres réels donc
On obtient un résultat qui ne contient que des nombres réels donc 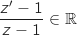 .
Pour
.
Pour 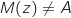 et
et 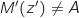 , on remarque que
, on remarque que 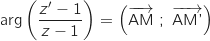 , or
, or
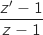 est réel, dont un argument est 0 ou
est réel, dont un argument est 0 ou 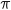 , soit
, soit 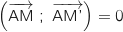 ou
ou 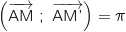 ce qui justifie que A,
ce qui justifie que A, 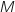 et
et 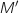 sont alignés.
sont alignés.
 .
.
Le point D' est sur  et est aligné avec A et D, donc D' est à l'intersection du cercle
et est aligné avec A et D, donc D' est à l'intersection du cercle  et de la droite (AD).
et de la droite (AD).
 et est aligné avec A et D, donc D' est à l'intersection du cercle
et est aligné avec A et D, donc D' est à l'intersection du cercle  et de la droite (AD).
et de la droite (AD).
