Corrigé de l'exercice 2 du bac S de maths d'avril 2013 à Pondichéry
Cacher les corrigés
Pour chacune des questions, quatre propositions de réponse sont données dont une seule est exacte. Pour chacune des questions indiquer, sans justification, la bonne réponse sur la copie. Une réponse exacte rapporte 1 point. Une réponse fausse ou l'absence de réponse ne rapporte ni n'enlève aucun point. Il en est de même dans le cas où plusieurs réponses sont données pour une même question.
L'espace est rapporté à un repère orthonormal.
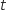et 
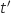désignent des paramètres réels.
Le plan (P) a pour équation 
.
Le plan (S) a pour représentation paramétrique : 
La droite (D) a pour représentation paramétrique : 
On donne les points de l'espace M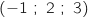
et N
.
1. Une représentation paramétrique du plan (P) est :
a) 
b) 
c) 
d) 
On peut déjà éliminer la réponse a) qui est la représentation paramétrique d'une droite.
Le plan de la proposition b) passe par le point de coordonnées 
(on prend 
dans la représentation paramétrique).
On regarde si les coordonnées de ce point vérifient l'équation cartésienne du plan (P) :
Donc la réponse b. est une « bonne candidate ».
Le plan de la proposition c) passe par 
et 
, donc la proposition c) ne peut pas être bonne.
Le plan de la proposition d) passe par 
et 
, donc la proposition d) ne peut pas être bonne.
Par élimination la bonne réponse ne peut être que b).
(on prend dans la représentation paramétrique).
On regarde si les coordonnées de ce point vérifient l'équation cartésienne du plan (P) :
Donc la réponse b. est une « bonne candidate ».
Le plan de la proposition c) passe par et , donc la proposition c) ne peut pas être bonne.
Le plan de la proposition d) passe par et , donc la proposition d) ne peut pas être bonne.
Par élimination la bonne réponse ne peut être que b).
2. a) La droite (D) et le plan (P) sont sécants au point A
.
b) La droite (D) et le plan (P) sont perpendiculaires.
c) La droite (D) est une droite du plan (P).
d) La droite (D) et le plan (P) sont strictement parallèles.
Les coordonnées de A ne verifient pas l'équation cartésienne de (P) :
Donc on peut éliminer la réponse a).
Par lecture sur la représentation paramétrique, un vecteur directeur de (D) est 
.
Par lecture sur l'équation cartésienne, un vecteur normal du plan (P) est 
.
Les coordonnées des 2 vecteurs ne sont pas proportionnelles donc ils ne sont pas colinéaires et du coup (D) n'est pas perpendiculaire à (P).
Donc la réponse b) n'est pas bonne.
Les réponses c) et d) impliquent que (D) est parallèle à (P), donc c'est pas la peine de le vérifier. Pour trancher entre les deux on regarde si le point
de coordonnées 
de la droite (obtenu en prenant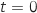 
dans la représentation paramétrique) appartient au plan :
Donc (D) est incluse dans (P), la bonne réponse est la c).
3. a) La droite (MN) et la droite (D) sont orthogonales.
b) La droite (MN) et la droite (D) sont parallèles.
c) La droite (MN) et la droite (D) sont sécantes.
d) La droite (MN) et la droite (D) sont confondues.
Donc on peut éliminer la réponse a).
Par lecture sur la représentation paramétrique, un vecteur directeur de (D) est .
Par lecture sur l'équation cartésienne, un vecteur normal du plan (P) est .
Les coordonnées des 2 vecteurs ne sont pas proportionnelles donc ils ne sont pas colinéaires et du coup (D) n'est pas perpendiculaire à (P).
Donc la réponse b) n'est pas bonne.
Les réponses c) et d) impliquent que (D) est parallèle à (P), donc c'est pas la peine de le vérifier. Pour trancher entre les deux on regarde si le point
de coordonnées de la droite (obtenu en prenant 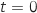dans la représentation paramétrique) appartient au plan :
Donc (D) est incluse dans (P), la bonne réponse est la c).
Un vecteur directeur de (MN) est 
soit
.
Un vecteur directeur de (D) est
On remarque déjà facilement que 
et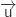 
ne sont pas colinéaires ce qui permet d'éliminer les réponses b) et d).
On calcule maintenant : 
.
Donc (MN) et (D) sont orthogonales. La bonne réponse est la réponse a).
4. a) Les plans (P) et (S) sont parallèles.
b) La droite soit
.
Un vecteur directeur de (D) est
On remarque déjà facilement que et 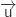ne sont pas colinéaires ce qui permet d'éliminer les réponses b) et d).
On calcule maintenant : .
Donc (MN) et (D) sont orthogonales. La bonne réponse est la réponse a).
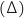de représentation paramétrique 
est la droite d'intersection des plans (P) et (S).
c) Le point M appartient à l'intersection des plans (P) et (S).
d) Les plans (P) et (S) sont perpendiculaires.
Il est plus simple de travailler avec les équations cartésiennes de plans. On détermine donc une équation cartésienne de (S) à partir
de la représentation paramétrique. Ce travail de départ permettra d'aller plus vite ensuite.
M
(S)
Donc une équation cartésienne de (S) est 
.
Un vecteur normal de (P) est
Un vecteur normal de (S) est 
Ces vecteurs ne sont pas colinéaires donc les plans ne sont pas parallèles et on élimine la réponse a).
Les points de 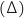sont de la forme 
avec 
. On regarde si les points de cette forme vérifient les équations
cartésiennes de (P) et (S).
Pour (P) : 
Pour (S) : 
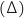Donc est incluse dans (P) et dans (S), c'est donc la droite d'intersection des ces 2 plans.
La bonne réponse est la réponse b).
(S)
Donc une équation cartésienne de (S) est .
Un vecteur normal de (P) est
Un vecteur normal de (S) est
Ces vecteurs ne sont pas colinéaires donc les plans ne sont pas parallèles et on élimine la réponse a).
Les points de 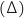sont de la forme avec . On regarde si les points de cette forme vérifient les équations
cartésiennes de (P) et (S).
Pour (P) :
Pour (S) :
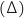Donc est incluse dans (P) et dans (S), c'est donc la droite d'intersection des ces 2 plans.
La bonne réponse est la réponse b).
