Corrigé de l'exercice 3 du bac S de maths d'avril 2013 à Pondichéry
Cacher les corrigés
Le plan complexe est muni d'un repère orthonormé direct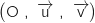
.
On note 
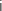le nombre complexe tel que 
.
On considère le point A d'affixe 
et le point B d'affixe 
.
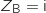A tout point M d'affixe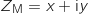 
, avec 
et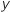 
deux réels tels que 
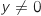, on associe le point M' d'affixe 
.
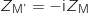On désigne par I le milieu du segment [AM].
Le but de l'exercice est de montrer que pour tout point M n'appartenant pas à (OA), la médiane (OI) du triangle OAM est aussi
une hauteur du triangle OBM' (propriété 1) et que BM'=2OI (propriété 2).
1. Dans cette question et uniquement dans cette question, on prend
.
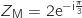a. Déterminer la forme algébrique de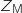 
.
.
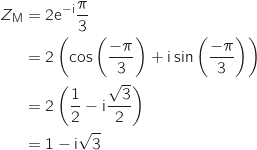
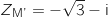Déterminer le module et un argument de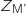 
.
.
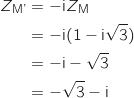
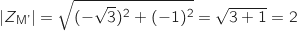Donc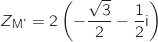 
Pour déterminer un argument de 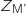on cherche une mesure 
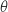telle que 
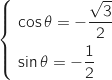On peut prendre 
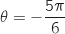, donc 
.
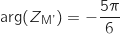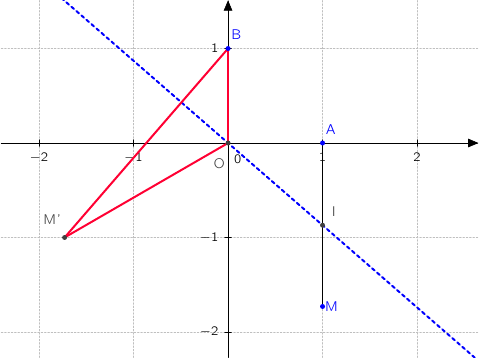
c. Placer les points A, B, M, M' et I dans le repère
en prenant 2 cm pour unité graphique.
Tracer la droite (OI) et vérifier rapidement les propriétés 1 et 2 à l'aide du graphique.
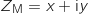avec .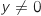
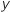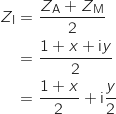
a. Déterminer l'affixe du point I en fonction de et .
et .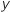
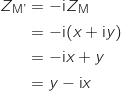
D'après ce qui précède on a directement :
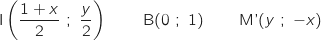
d. Montrer que la droite (OI) est une hauteur du triangle OBM'.
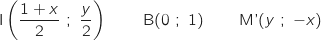
Si la droite (OI) est une hauteur de OBM' alors c'est la hauteur issue de O relative au côté [BM']. Il faut donc vérifier
que (OI) est perpendiculaire à (BM').
On calcule les coordonnées des vecteurs :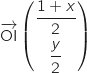 
et
.
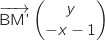On utilise la formule du produit scalaire en repère orthonormé :
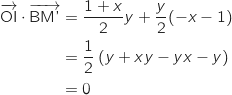Du coup les vecteurs 
et 
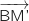sont orthogonaux et les droites (OI) et (BM') sont perpendiculaires ce qui
montre que (OI) est une hauteur du triangle OBM'.
e. Montrer que BM'=2OI.
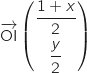et
.
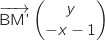On utilise la formule du produit scalaire en repère orthonormé :
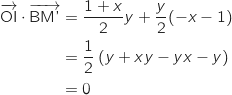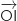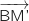Du coup les vecteurs et sont orthogonaux et les droites (OI) et (BM') sont perpendiculaires ce qui
montre que (OI) est une hauteur du triangle OBM'.
On calcule les normes des vecteurs 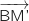et :
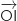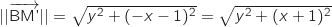
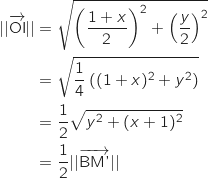Ainsi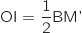 
ou encore BM'=2OI.
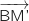et :
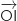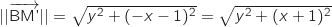
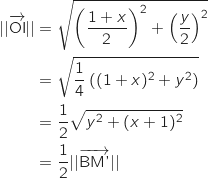Ainsi 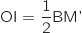ou encore BM'=2OI.
