Corrigé de l'exercice de spécialité du bac S de maths d'avril 2013 à Pondichéry
Cacher les corrigés
On étudie l'évolution dans le temps du nombre de jeunes et d'adultes dans une population d'animaux. Pour tout entier naturel
, on note 
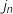le nombre d'animaux jeunes après années d'observation et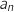 
le nombre d'animaux adultes après années d'observation.
Il y a au début de la première année de l'étude, 200 animaux jeunes et 500 animaux adultes.
Ainsi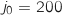 
et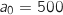 
.
On admet que pour tout entier naturel on a :
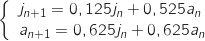
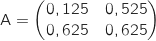et, pour tout entier naturel , 
.
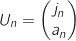1.a. Montrer que pour tout entier naturel
, 
.
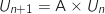Pour tout entier naturel , on effectue le produit des matrices :
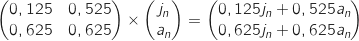On a donc : 
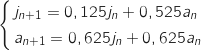ce qui correspond bien aux données de l'énoncé.
b. Calculer le nombre d'animaux jeunes et d'animaux adultes après un an d'observation puis après deux ans d'observation (résultats arrondis à l'unité près par défaut).
, on effectue le produit des matrices :
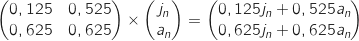On a donc :
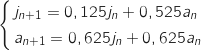ce qui correspond bien aux données de l'énoncé.
.
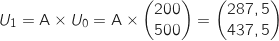Donc, à l'unité près par défaut, après un an le nombre de jeunes est de 287 et d'adultes est de 437.
.
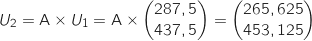Donc après deux ans il y a 265 jeunes et 453 adultes.
non nul, exprimer 
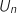en fonction de 
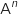et de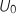 
.
.
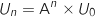2. On introduit les matrices suivantes
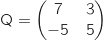et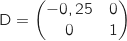 
.
a. On admet que la matrice Q est inversible et que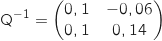 
.
Montrer que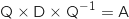 
.
On effectue d'abord le produit :
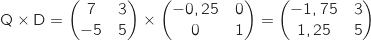puis on vérifie que :
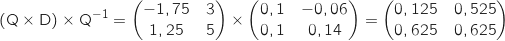
b. Montrer par récurrence sur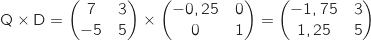
puis on vérifie que :
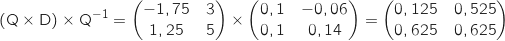
que pour tout entier naturel non nul :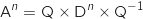 
.
La propriété à montrer pour tout entier naturel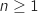 
est :
: « 
»
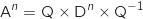Initialisation au rang 1
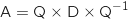(vu dans le a.)
Hérédité
On suppose que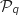 
est vraie pour un rang 
: 
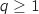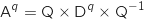On montre qu'alors 
est également vraie.
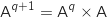On remplace 
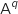par 
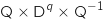(hypothèse de récurrence) et on remplace
A par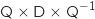 
, il vient :
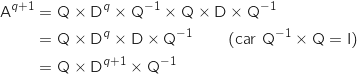Donc est vraie.
Ainsi est vraie pour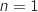 
et est héréditaire, donc est vraie pour tout entier .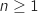
c. Pour tout entier naturel 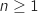est :
: « »
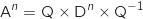Initialisation au rang 1
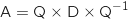(vu dans le a.)
Hérédité
On suppose que 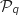est vraie pour un rang :
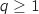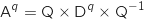On montre qu'alors est également vraie.
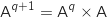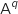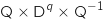On remplace par (hypothèse de récurrence) et on remplace
A par 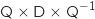, il vient :
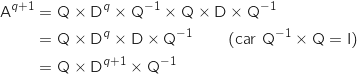Donc est vraie.
Ainsi est vraie pour 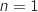et est héréditaire, donc est vraie pour tout entier .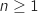
non nul, déterminer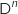 
en fonction de .
La matrice D étant diagonale on a directement :
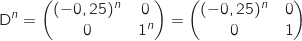
3. On admet que pour tout entier nature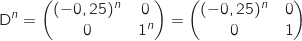l
non nul,
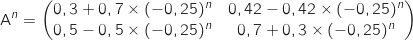
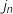et 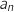en fonction de et déterminer les limites de ces deux suites.
Pour tout entier naturel :
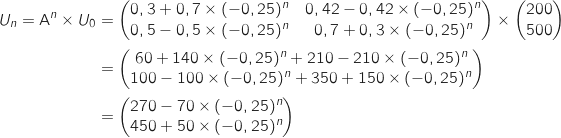Donc 
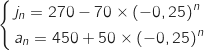Comme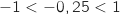 
on a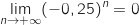 
et du coup 
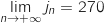et
.
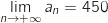b. Que peut-on en conclure pour la population d'animaux étudiée ?
:
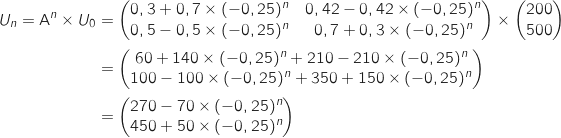Donc
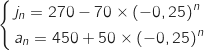Comme 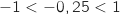on a 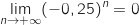et du coup 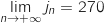et
.
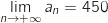Au cours du temps la population d'animaux tend à se stabiliser vers 270 jeunes et 450 adultes.
