Corrigé de l'exercice 3 du bac S de maths d'avril 2014 à Pondichéry
Cacher les corrigés
Le plan complexe est muni d'un repère orthonormé . Pour tout entier naturel , on note A le point d'affixe défini par : et On définit la suite par pour tout entier naturel . 1. Donner la forme exponentielle du nombre complexe .
2.a. Montrer que la suite est géométrique de raison .
Pour tout entier naturel :
Donc et est bien géométrique de raison .
b. En déduire l'expression de en fonction de .
, car .
c. Que dire de la longueur OA lorsque tend vers ?
, or la raison de la suite géométrique est strictement comprise entre et , donc la longueur considérée tend vers 0.
3. On considère l'algorithme suivant :
| Variables | entier naturel réel réel strictement positif |
| Entrée | Demander la valeur de |
| Traitement | prend la valeur 1 prend la valeur 0 Tant que prend la valeur prend la valeur Fin tant que |
| Sortie | Afficher |
| Initialisation | 1 | 0 |
| itération 1 | 1 | |
| itération 2 | 2 | |
| itération 3 | 3 | |
| itération 4 | 4 | |
| itération 5 | 5 |
L'algorithme affiche le rang du premier terme de la suite qui est inférieur ou égal à .
4.a. Démontrer que le triangle est rectangle en .
Donc
Par la propriété de Pythagore cela montre que est rectangle en .
b. On admet que .
Déterminer les valeurs de pour lesquelles est un point de l'axe des ordonnées.
est sur l'axe des ordonnées équivaut à est imaginaire pur :
avec .
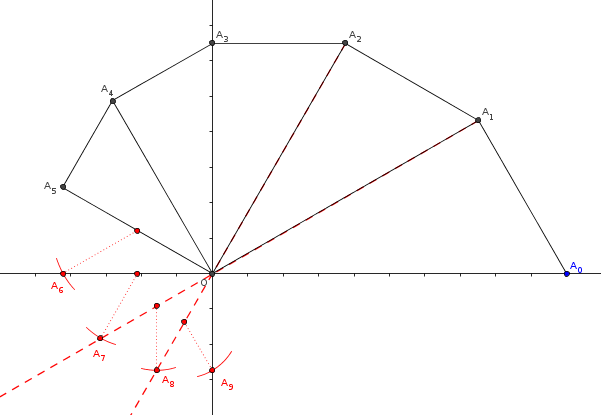
c. Compléter la figure donnée ci-dessous en représentant les points ,
, et .
Les traits de construction seront apparents.