Corrigé de l'exercice 4 du bac S de maths d'avril 2014 à Pondichéry
Cacher les corrigés
Partie A
est une fonction définie et dérivable sur . est la fonction dérivée de la fonction . Dans le plan muni d'un repère orthogonal, on nomme la courbe représentative de la fonction et la courbe représentative de la fonction . Le point A de coordonnées appartient à la courbe . Le point B de coordonnées appartient à la courbe .
1. Dans les trois situations ci-dessous, on a dessiné la courbe représentative de la fonction . Sur l'une d'entre elles, la courbe de la fonction dérivée est tracée convenablement. Laquelle ? Expliquer le choix effectué.
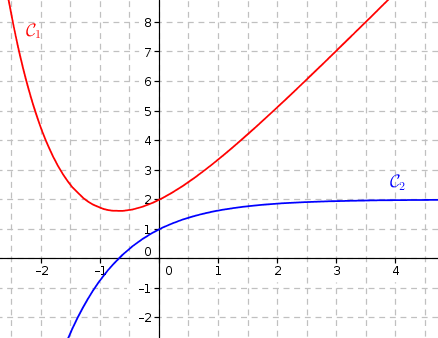
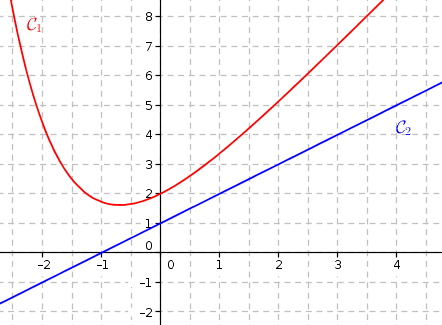
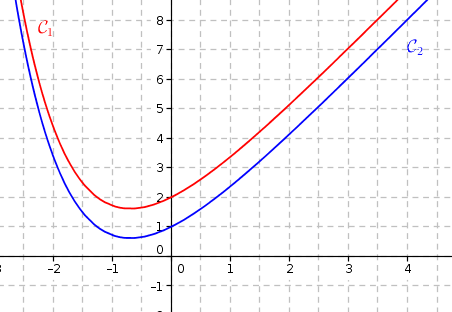
Le signe de la fonction représentée par doit être compatible avec les variations de la fonction représentée par .
Situation 1 : Ok !
Situation 2 : presque bon, mais il y a un "petit décalage"
Situation 3 : ça va pas du tout !
Donc la bonne réponse est la situation 1.
2. Déterminer l'équation réduite de la droite tangente à la courbe en A.
A entraîne que
B entraîne que
Equation de : soit
3. On sait que pour tout réel , où et
sont deux nombres réels.
a. Déterminer la valeur de en utilisant les renseignements donnés par l'énoncé.
donc
b. Prouver que .
est dérivable sur et .
Or , donc
4. Etudier les variations de la fonction sur .
On a .
.
De même : et
Tableau de variations :
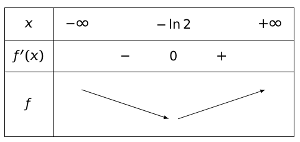
5. Déterminer la limite de la fonction en .

- ; donc
Partie B
Soit la fonction définie sur par . 1.a. Montrer que la fonction admet 0 comme minimum sur .
est dérivable sur et .
.
De même : et .
Tableau de variations :
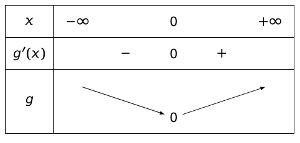
où .
Donc admet comme minimum sur .
b. En déduire la position de la courbe par rapport à la droite .

D'après a., pour tout : soit
.
Donc est située au dessus de .
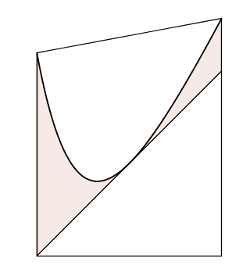
La figure ci-dessous représente le logo d'une entreprise.
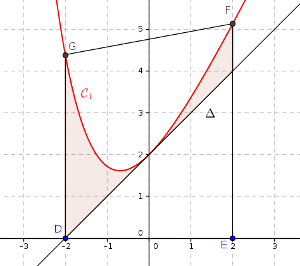
- D est le point de coordonnées ,
- E est le point de coordonnées ,
- F est le point d'abscisse 2 de la courbe ,
- G est le point d'abscisse de la courbe
L'aire du domaine est donnée par :
