Sujet et corrigé de l'exercice 1 du bac S de maths d'avril 2015 à Pondichéry
Cacher les corrigés
PARTIE A
Soit la fonction définie sur par .
Sur le graphique ci-après, on a tracé dans un repère orthogonal , la courbe réprésentative de la fonction et la droite d'équation .
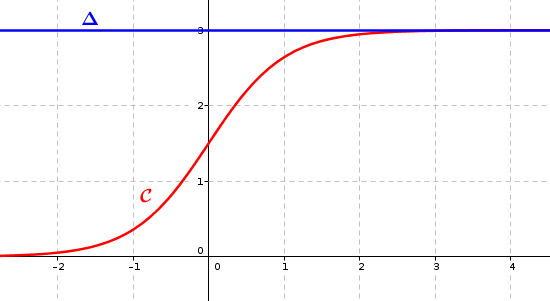
1. Démontrer que la fonction est strictement croissante sur .
La fonction est dérivable sur et on peut écrire :
avec :
;
Donc
Pour tout :
donc , ce qui prouve que est strictement croissante sur .
2. Justifier que la droite est asymptote à la courbe .
On détermine la limite de en :
; , donc par composition : et en ajoutant 1 :
Finalement par quotient : .
Ce résultat de limite justifie que la droite d'équation est asymptote à la courbe en .
3. Démontrer que l'équation admet une unique solution sur .
Déterminer un encadrement de d'amplitude .
La fonction est continue et strictement croissante sur , avec :
Comme , d'après le théorème de la valeur intermédiaire, l'équation admet une unique solution dans .
On notera que l'équation ne peut pas avoir de solution dans , car sur cet intervalle le maximum de la fonction est , donc l'équation admet bien une unique solution sur .
Par balayage on trouve l'encadrement : .
PARTIE B
Soit la fonction définie sur par .
1. Justifier que la fonction est positive sur .
D'après l'étude précédente est strictement croissante et de limite 3 en , donc est majorée par sur , du coup pour tout :
ce qui donne et donc .
2. On désigne par la fonction définie sur par .
Démontrer que est une primitive de sur .
La fonction proposée est dérivable sur et on a :
où
;
Donc
D'autre part :
Du coup on a bien pour tout : , ce qui montre que est une primitive de sur .
3. Soit un réel strictement positif.
a. Donner une interprétation graphique de l'intégrale .
Comme (bornes dans le bon ordre), et comme , l'intégrale représente l'aire du domaine délimité par :
la droite ,
la courbe ,
les droites d'équations et .
b. Démontrer que .
c. On note l'ensemble des points du plan défini par .
Déterminer l'aire, en unité d'aire, du domaine .
Il s'agit de calculer :
(voir question A.2), donc par quotient : .
Du coup : u.a.
