Sujet et corrigé de l'exercice 4 du bac S de maths d'avril 2015 à Pondichéry
Cacher les corrigés
Soit un cube ABCDEFGH d'arête 1.
Dans le repère , on considère les points M, N et P de coordonnées respectives :
M N P
1. Placer M, N et P sur la figure ci-dessous.
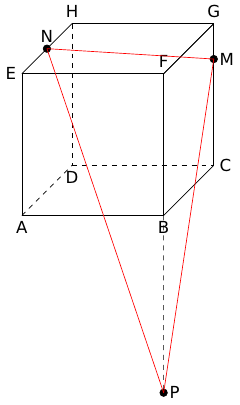
2. Déterminer les coordonnées des vecteurs et .
En déduire que les points M, N et P ne sont pas alignés.
soit
soit
On remarque que les coordonnées de ne sont pas proportionnelles à celles de , donc les vecteurs ne sont pas colinéaires et par conséquent les points M, N et P ne sont pas alignés.
3. On considère l'algorithme 1 donné ci-dessous :
| Saisir |
| prend la valeur |
| prend la valeur |
| prend la valeur |
| prend la valeur |
| prend la valeur |
| prend la valeur |
| prend la valeur |
| Afficher |
a. Exécuter à la main cet algorithme avec les coordonnées des points M, N et P données ci- dessus.
| -1 | |
| 0 | |
b. A quoi correspond le résultat affiché par l'algorithme ? Qu'en déduire pour le triangle MNP ?
Le résultat affiché correspond au produit scalaire : .
Comme on obtient 0, cela signifie que les vecteurs et sont orthogonaux et que le triangle MNP est rectangle en M.
4. On considère l'algorithme donné ci-dessous. Le compléter pour qu'il teste et affiche si un triangle MNP est rectangle et isocèle en M.
| Saisir |
| prend la valeur |
| prend la valeur |
| prend la valeur |
| prend la valeur |
| prend la valeur |
| prend la valeur |
| prend la valeur |
| ... |
| prend la valeur |
| prend la valeur |
| Si et alors |
| Afficher "Le triangle est rectangle isocèle en M" |
| Sinon |
| Afficher "Le triangle n'est pas rectangle isocèle en M" |
| Fin Si |
5. On considère le vecteur normal au plan (MNP).
a. Déterminer une équation cartésienne du plan (MNP).
Une équation cartésienne du plan (MNP) s'écrit sous la forme :
Pour trouver , on utilise le fait que, par exemple, M appartient au plan ce qui donne :
Donc une équation cartésienne du plan est : .
b. On considère la droite passant par F et de vecteur directeur .
Déterminer une représentation paramétrique de la droite .
Les coordonnées de F sont et on a directement :
où le paramètre décrit .
6. Soit K le point d'intersection du plan (MNP) et de la droite .
a. Démontrer que les coordonnées du point K sont .
Comme on nous donne les coordonnées du point d'intersection, il suffit de vérifier que le point de coordonnées appartient à la fois au plan et à la droite.
Au plan
, donc ce point appartient au plan.
A la droite
On cherche le paramètre éventuel tel que :
Le système admet une unique solution, donc ce point appartient à la droite.
Ainsi le point de coordonnées est commun au plan(MNP) et à la droite qui se coupent en K, donc .
b. On donne FK.
Calculer le volume du tétraèdre MNPF.
La droite (FK) est perpendiculaire au plan(MNP) et coupe le plan en K, donc la hauteur du tétraèdre de base (MNP) et de sommet K est FK.
Pour calculer le volume nous avons besoin de l'aire de la base, et comme le triangle MNP est rectangle en M il suffit de calculer :
Finalement le volume cherché est :
