Corrigé de l'exercice 1 du bac S de maths 2011 en Amérique du Nord
Cacher les corrigés
Cet exercice a été modifié afin d'être conforme au nouveau programme en vigueur à partir de l'année scolaire 2012-2013.
Le plan complexe est rapporté à un repère orthonormal direct 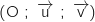 .
On considère les points A et B d'affixes respectives :
.
On considère les points A et B d'affixes respectives : 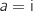 et
et 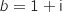 .
.
Partie A
On considère le point C d'affixe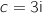 .
On note
.
On note 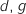 et
et 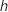 les affixes respectives des points D, G et H avec :
les affixes respectives des points D, G et H avec :
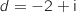
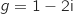
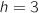 .
.
Démontrer que le quadrilatère CDGH est un rectangle.
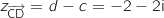
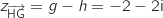 Donc
Donc 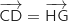 ce qui prouve que CDGH est un parallélogramme.
ce qui prouve que CDGH est un parallélogramme.
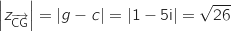 .
.
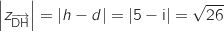 .
Du coup les diagonales du parallélogramme sont de même longueur, donc c'est un rectangle.
.
Du coup les diagonales du parallélogramme sont de même longueur, donc c'est un rectangle.
Partie B
On considère un point M, distinct de O et de A, d'affixe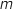 .
On note
.
On note 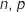 et
et  les affixes respectives des points N, P et Q avec :
les affixes respectives des points N, P et Q avec :
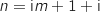
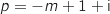
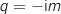 1. Montrer que le quadrilatère MNPQ est un parallélogramme.
1. Montrer que le quadrilatère MNPQ est un parallélogramme.
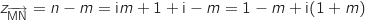 .
.
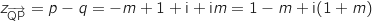 .
Donc
.
Donc 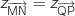 , ce qui montre que MNPQ est
un parallélogramme.
, ce qui montre que MNPQ est
un parallélogramme.
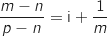 .
.
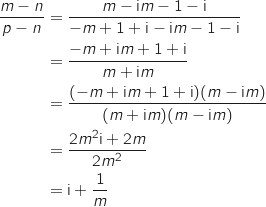
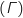 des points M tels que le quadrilatère MNPQ soit un rectangle.
des points M tels que le quadrilatère MNPQ soit un rectangle.
MNPQ est rectangle signifie que 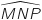 est droit ce qui équivaut traduit avec les affixes à
est droit ce qui équivaut traduit avec les affixes à 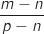 imaginaire pur.
Comme
imaginaire pur.
Comme 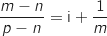 , ce dernier est imaginaire pur si et seulement si
, ce dernier est imaginaire pur si et seulement si
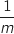 est lui même imaginaire pur, soit
est lui même imaginaire pur, soit 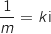 , d'où
, d'où 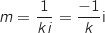 .
Lorsque
.
Lorsque  , décrit
, décrit  , l'ensemble des points M d'affixe
, l'ensemble des points M d'affixe 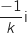 , décrit l'axe des ordonnées privé de l'origine.
Donc l'ensemble
, décrit l'axe des ordonnées privé de l'origine.
Donc l'ensemble 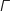 est l'axe des ordonnées privé de O et de A (on n'oublie pas que M
est l'axe des ordonnées privé de O et de A (on n'oublie pas que M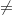 A).
A).
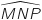 est droit ce qui équivaut traduit avec les affixes à
est droit ce qui équivaut traduit avec les affixes à 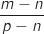 imaginaire pur.
Comme
imaginaire pur.
Comme 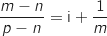 , ce dernier est imaginaire pur si et seulement si
, ce dernier est imaginaire pur si et seulement si
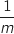 est lui même imaginaire pur, soit
est lui même imaginaire pur, soit 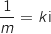 , d'où
, d'où 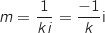 .
Lorsque
.
Lorsque  , décrit
, décrit  , l'ensemble des points M d'affixe
, l'ensemble des points M d'affixe 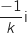 , décrit l'axe des ordonnées privé de l'origine.
Donc l'ensemble
, décrit l'axe des ordonnées privé de l'origine.
Donc l'ensemble 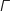 est l'axe des ordonnées privé de O et de A (on n'oublie pas que M
est l'axe des ordonnées privé de O et de A (on n'oublie pas que M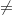 A).
A).
