Corrigé de l'exercice 2 du bac S de maths 2011 en Amérique du Nord
Cacher les corrigés
Partie A
Une salle informatique d'un établissement scolaire est équipée de 25 ordinateurs dont 3 sont défectueux. Tous les ordinateurs ont la même probabilité d'être choisis. On choisit au hasard deux ordinateurs de cette salle. Quelle est la probabilité que ces deux ordinateurs soient défectueux ?
Le choix au hasard des deux ordinateurs équivaut au tirage successif sans remise de deux ordinateurs.
Soit A l'événement : « le premier ordinateur tiré est défectueux »
et B l'événement : « le deuxième ordinateur tiré est défectueux ».
On peut alors représenter la situation par l'arbre de probabilités :
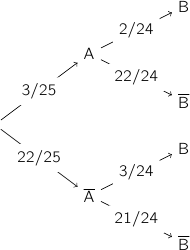
L'événement considéré correspond à 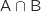 et
en utilisant la formule des probabilités composées (principe multiplicatif sur l'arbre) on a :
et
en utilisant la formule des probabilités composées (principe multiplicatif sur l'arbre) on a :
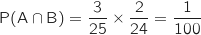 .
.

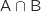 et
en utilisant la formule des probabilités composées (principe multiplicatif sur l'arbre) on a :
et
en utilisant la formule des probabilités composées (principe multiplicatif sur l'arbre) on a :
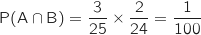 .
.
Partie B
La durée de vie d'un ordinateur (c'est-à-dire la durée de fonctionnement avant la première panne), est une variable aléatoire qui suit une loi exponentielle de paramètre
qui suit une loi exponentielle de paramètre 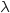 avec
avec 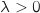 .
Ainsi, pour tout réel
.
Ainsi, pour tout réel 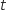 positif, la probabilité qu'un ordinateur ait une durée de vie inférieure à
positif, la probabilité qu'un ordinateur ait une durée de vie inférieure à 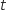 années, notée
années, notée 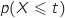 , est donnée par :
, est donnée par : 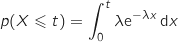 .
1. Déterminer
.
1. Déterminer 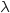 sachant que
sachant que 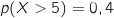 .
.
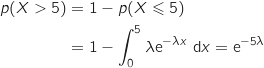 Donc on doit résoudre :
Donc on doit résoudre : 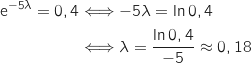
2. Dans cette question, on prendra
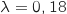 .
Sachant qu'un ordinateur n'a pas eu de panne au cours des 3 premières années, quelle est, à
.
Sachant qu'un ordinateur n'a pas eu de panne au cours des 3 premières années, quelle est, à 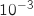 près, la probabilité qu'il ait une durée de vie supérieure à 5 ans ?
près, la probabilité qu'il ait une durée de vie supérieure à 5 ans ?
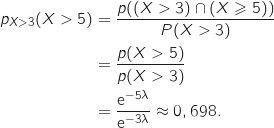
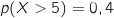 .
a. On considère un lot de 10 ordinateurs.
Quelle est la probabilité que, dans ce lot, l'un au moins des ordinateurs ait une durée de vie supérieure à 5 ans ? On donnera une valeur arrondie au millième de cette probabilité.
.
a. On considère un lot de 10 ordinateurs.
Quelle est la probabilité que, dans ce lot, l'un au moins des ordinateurs ait une durée de vie supérieure à 5 ans ? On donnera une valeur arrondie au millième de cette probabilité.
En utilisant l'événement contraire : « tous les ordinateurs ont une durée de vie inférieure à 5 ans » on a directement la probabilité demandée en utilisant une loi binomiale à savoir :
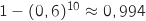 .
.
b. Quel nombre minimal d'ordinateurs doit-on choisir pour que la probabilité de l'évènement « l'un au moins d'entre eux a une durée de vie supérieure à 5 ans » soit supérieure à 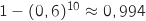 .
.
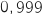 ?
?
On doit résoudre : 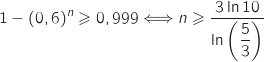 avec
avec 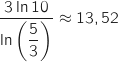 , donc il faut prendre au minimum 14 ordinateurs.
, donc il faut prendre au minimum 14 ordinateurs.
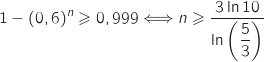 avec
avec 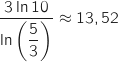 , donc il faut prendre au minimum 14 ordinateurs.
, donc il faut prendre au minimum 14 ordinateurs.
