Corrigé de l'exercice 3 du bac S de maths 2011 en Amérique du Nord
Cacher les corrigés
Partie A : Restitution organisée de connaissances
Dans le sujet initial cette partie traitait de sphère et de barycentre, notions qui ne sont plus au programme à partir
de l'année scolaire 2012-2013.
Partie B
On considère le cube ABCDEFGH d'arête de longueur 1 représenté ci-dessous.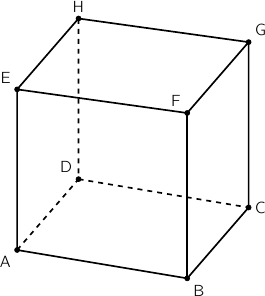
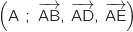 .
1. Démontrer que le vecteur
.
1. Démontrer que le vecteur 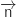 de coordonnées
de coordonnées 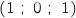 est un vecteur normal au plan (BCE).
est un vecteur normal au plan (BCE).
Deux vecteurs non colinéaires du plan sont : 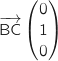 et
et 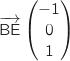 .
On a en utilisant la formule du produit scalaire :
.
On a en utilisant la formule du produit scalaire : 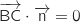 et
et 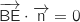 .
Donc
.
Donc  est normal au plan.
est normal au plan.
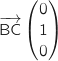 et
et 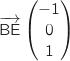 .
On a en utilisant la formule du produit scalaire :
.
On a en utilisant la formule du produit scalaire : 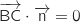 et
et 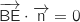 .
Donc
.
Donc  est normal au plan.
est normal au plan.
2. Déterminer une équation du plan (BCE).
En utilisant le vecteur normal de la question précédente, on sait que le plan (BCE) admet
une équation de la forme :
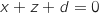
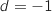 .
Finalement une équation du plan est :
.
Finalement une équation du plan est : 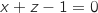 .
.
3. On note 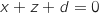
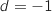 .
Finalement une équation du plan est :
.
Finalement une équation du plan est : 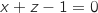 .
.
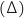 la droite perpendiculaire en E au plan (BCE).
Déterminer une représentation paramétrique de la droite
la droite perpendiculaire en E au plan (BCE).
Déterminer une représentation paramétrique de la droite 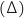 .
.
Un vecteur directeur de 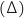 est
est  d'où la représentation paramétrique :
d'où la représentation paramétrique : 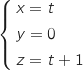
4. Démontrer que la droite 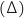 est
est  d'où la représentation paramétrique :
d'où la représentation paramétrique : 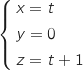
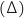 est sécante au plan (ABC) en un point R, symétrique de B par rapport à A.
est sécante au plan (ABC) en un point R, symétrique de B par rapport à A.
On résout : 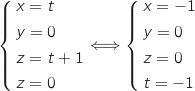 Donc R
Donc R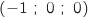 .
Pour la symétrie, on vérifie que A est bien au milieu de [RB] :
.
Pour la symétrie, on vérifie que A est bien au milieu de [RB] : 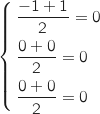
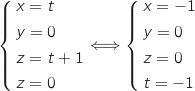 Donc R
Donc R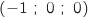 .
Pour la symétrie, on vérifie que A est bien au milieu de [RB] :
.
Pour la symétrie, on vérifie que A est bien au milieu de [RB] : 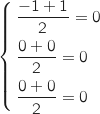
La dernière question du sujet original portait sur des notions qui ne figurent plus au programme à partir de la session 2013
du baccalauréat.
