Corrigé de l'exercice 1 du bac S de maths 2011 dans les centres étrangers
Cacher les corrigés
On considère une droite munie d'un repère
munie d'un repère 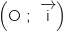 .
Soit
.
Soit 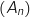 la suite de points de la droite
la suite de points de la droite  ainsi définie :
ainsi définie :
-
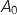 est le point O ;
est le point O ;
-
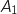 est le point d'abscisse
est le point d'abscisse 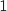 ;
;
- pour tout entier naturel
 , le point
, le point 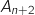 est le milieu du segment
est le milieu du segment 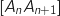 .
.
 , les points
, les points 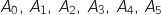 et
et 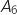 .
On prendra 10 cm comme unité graphique.
.
On prendra 10 cm comme unité graphique.

b. Pour tout entier naturel
 , on note
, on note 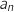 l'abscisse du point
l'abscisse du point 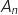 .
Calculer
.
Calculer 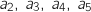 et
et 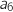 .
.
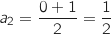
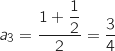
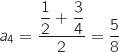
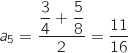
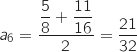
c. Pour tout entier naturel
 , justifier l'égalité :
, justifier l'égalité : 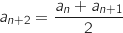 .
.
Cette formule est immédiate : c'est la formule de l'abscisse du milieu de deux points.
2. Démontrer par récurrence, que pour tout entier 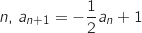 .
.
La propriété à montrer pour tout entier 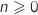 est :
est :
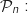 «
«
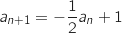 ».
Initialisation
».
Initialisation
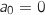 ,
, 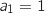 , et
, et 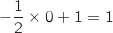 , soit
, soit 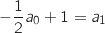 .
Donc
.
Donc 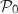 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang 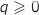 , on a donc l'hypothèse de récurrence :
, on a donc l'hypothèse de récurrence :
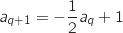 On montre qu'alors la propriété est vraie au rang
On montre qu'alors la propriété est vraie au rang 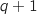 .
D'après la définition de la suite :
.
D'après la définition de la suite :
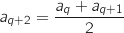 On remplace
On remplace 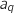 en utilisant l'hypothèse de récurrence :
en utilisant l'hypothèse de récurrence :  .
.
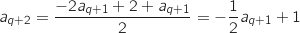 .
Donc
.
Donc  est vraie.
Ainsi la propriété est vraie au rang
est vraie.
Ainsi la propriété est vraie au rang 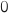 et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier
et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier 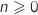 .
.
3. Soit 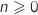 est :
est :
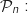 «
«
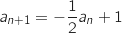 ».
Initialisation
».
Initialisation
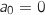 ,
, 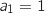 , et
, et 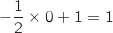 , soit
, soit 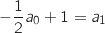 .
Donc
.
Donc 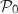 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang 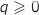 , on a donc l'hypothèse de récurrence :
, on a donc l'hypothèse de récurrence :
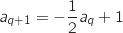 On montre qu'alors la propriété est vraie au rang
On montre qu'alors la propriété est vraie au rang 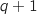 .
D'après la définition de la suite :
.
D'après la définition de la suite :
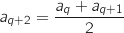 On remplace
On remplace 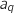 en utilisant l'hypothèse de récurrence :
en utilisant l'hypothèse de récurrence :  .
.
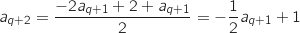 .
Donc
.
Donc  est vraie.
Ainsi la propriété est vraie au rang
est vraie.
Ainsi la propriété est vraie au rang 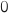 et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier
et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier 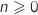 .
.
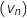 la suite définie, pour tout entier naturel
la suite définie, pour tout entier naturel  , par
, par
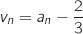
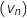 est une suite géométrique de raison
est une suite géométrique de raison 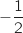 .
.
Pour tout entier naturel  , on a :
, on a :
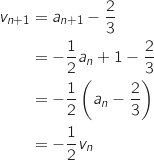 Donc la suite
Donc la suite  est une suite géométrique de raison
est une suite géométrique de raison 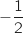 .
.
4. Déterminer la limite de la suite  , on a :
, on a :
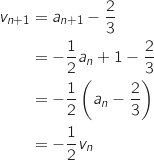 Donc la suite
Donc la suite  est une suite géométrique de raison
est une suite géométrique de raison 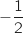 .
.
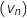 , puis celle de la suite
, puis celle de la suite 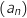 .
.
La raison de la suite géométrique  est comprise entre
est comprise entre 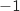 et
et 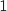 , donc cette suite converge vers 0.
En utilisant les règles de calcul sur les limites on a :
, donc cette suite converge vers 0.
En utilisant les règles de calcul sur les limites on a :
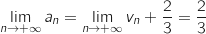 .
.
 est comprise entre
est comprise entre 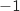 et
et 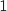 , donc cette suite converge vers 0.
En utilisant les règles de calcul sur les limites on a :
, donc cette suite converge vers 0.
En utilisant les règles de calcul sur les limites on a :
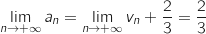 .
.
