Corrigé de l'exercice 4 du bac S de maths 2011 dans les centres étrangers
Cacher les corrigés
Soient et
et  les fonctions définies sur l'ensemble
les fonctions définies sur l'ensemble  des nombres réels par :
des nombres réels par :
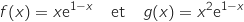
 et
et  dans un repère orthogonal
dans un repère orthogonal 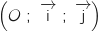 sont respectivement notées
sont respectivement notées  et
et 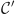 et sont données ci-dessous :
et sont données ci-dessous :
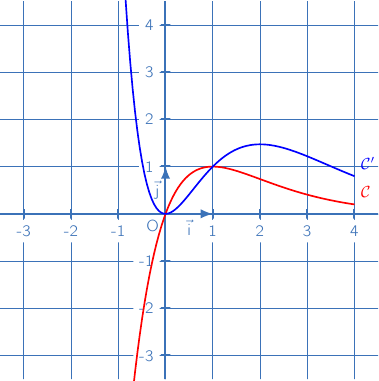
1. Etude des fonctions
 et
et a. Déterminer les limites des fonctions
a. Déterminer les limites des fonctions  et
et  en
en  .
.
Limite de la fonction  en
en 
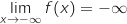 .
Limite de la fonction
.
Limite de la fonction  en
en 
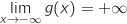 .
.
 en
en 
-
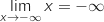 (fonction de
référence)
(fonction de
référence)
-
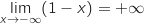 et par
composition :
et par
composition : 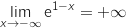
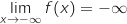 .
Limite de la fonction
.
Limite de la fonction  en
en 
-
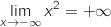 (fonction
de référence)
(fonction
de référence)
-
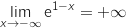
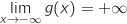 .
.
b. Justifier le fait que les fonctions
 et
et  ont pour limite
ont pour limite 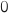 en
en  .
.
Limite de  en
en  On remarque qu'on a une forme indéterminée.
On écrit :
On remarque qu'on a une forme indéterminée.
On écrit : 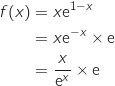 Cela a pour effet de faire apparaître la fonction de référence
Cela a pour effet de faire apparaître la fonction de référence 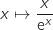 .
On sait d'après le cours (croissance comparée des fonctions exponentielles
et des fonctions puissances) que :
.
On sait d'après le cours (croissance comparée des fonctions exponentielles
et des fonctions puissances) que :
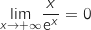 .
Donc par produit avec e, on a
.
Donc par produit avec e, on a 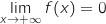 .
Limite de
.
Limite de  en
en  On est exactement dans le même cas et on procède de la même façon :
On est exactement dans le même cas et on procède de la même façon :
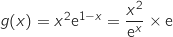 ,
avec
,
avec 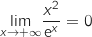 Donc par produit
Donc par produit 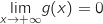 .
.
c. Etudier le sens de variations de chacune des fonctions  en
en  On remarque qu'on a une forme indéterminée.
On écrit :
On remarque qu'on a une forme indéterminée.
On écrit : 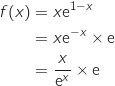 Cela a pour effet de faire apparaître la fonction de référence
Cela a pour effet de faire apparaître la fonction de référence 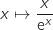 .
On sait d'après le cours (croissance comparée des fonctions exponentielles
et des fonctions puissances) que :
.
On sait d'après le cours (croissance comparée des fonctions exponentielles
et des fonctions puissances) que :
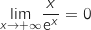 .
Donc par produit avec e, on a
.
Donc par produit avec e, on a 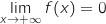 .
Limite de
.
Limite de  en
en  On est exactement dans le même cas et on procède de la même façon :
On est exactement dans le même cas et on procède de la même façon :
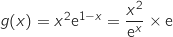 ,
avec
,
avec 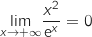 Donc par produit
Donc par produit 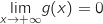 .
.
 et
et  et dresser leurs tableaux de variations respectifs.
et dresser leurs tableaux de variations respectifs.
Fonction  La fonction
La fonction  est définie et dérivable sur
est définie et dérivable sur  .
Pour trouver la fonction dérivée de
.
Pour trouver la fonction dérivée de  on utilise la formule de
la dérivée d'un produit :
on utilise la formule de
la dérivée d'un produit :
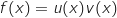 avec :
avec :
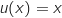 , donc
, donc 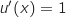
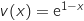 , donc
, donc 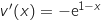
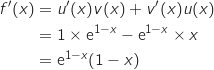 Comme pour tout
Comme pour tout  ,
, 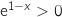 , le signe de
, le signe de
 est le même que celui de
est le même que celui de 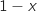 .
On a directement le tableau de signes :
.
On a directement le tableau de signes :
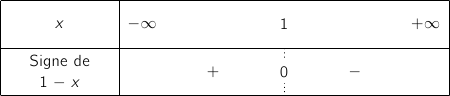
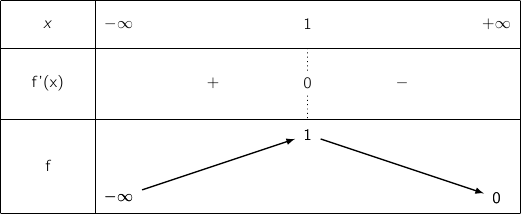
On en déduit le tableau de variations de  :
:
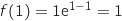 Fonction
Fonction  Comme
Comme  , la fonction
, la fonction  est définie et dérivable sur
est définie et dérivable sur  et on a :
et on a :
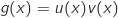 avec :
avec :
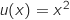 , donc
, donc 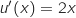
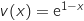 , donc
, donc 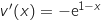
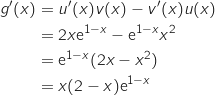 Le signe de
Le signe de 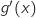 est le même que celui de
est le même que celui de 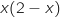 .
Il s'agit d'une expression polynôme du second degré dont les racines
sont 0 et 2, on a donc directement le tableau de signes :
.
Il s'agit d'une expression polynôme du second degré dont les racines
sont 0 et 2, on a donc directement le tableau de signes :

On en déduit le tableau de variations de  :
:
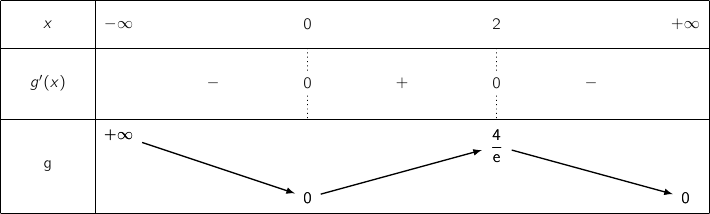
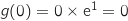
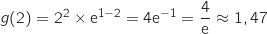
2. Calcul d'intégrales
Pour tout entier naturel  La fonction
La fonction  est définie et dérivable sur
est définie et dérivable sur  .
Pour trouver la fonction dérivée de
.
Pour trouver la fonction dérivée de  on utilise la formule de
la dérivée d'un produit :
on utilise la formule de
la dérivée d'un produit :
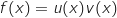 avec :
avec :
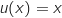 , donc
, donc 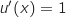
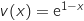 , donc
, donc 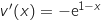
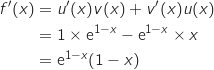 Comme pour tout
Comme pour tout  ,
, 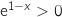 , le signe de
, le signe de
 est le même que celui de
est le même que celui de 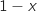 .
On a directement le tableau de signes :
.
On a directement le tableau de signes :

 :
:

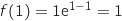 Fonction
Fonction  Comme
Comme  , la fonction
, la fonction  est définie et dérivable sur
est définie et dérivable sur  et on a :
et on a :
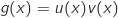 avec :
avec :
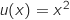 , donc
, donc 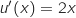
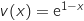 , donc
, donc 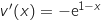
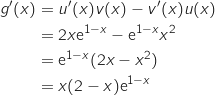 Le signe de
Le signe de 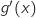 est le même que celui de
est le même que celui de 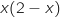 .
Il s'agit d'une expression polynôme du second degré dont les racines
sont 0 et 2, on a donc directement le tableau de signes :
.
Il s'agit d'une expression polynôme du second degré dont les racines
sont 0 et 2, on a donc directement le tableau de signes :

 :
:

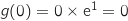
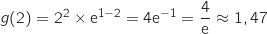
 , on définit l'intégrale
, on définit l'intégrale 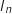 par :
par :
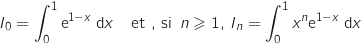
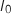 .
.
La fonction 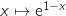 est définie et continue
sur
est définie et continue
sur 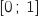 et admet pour primitive la fonction
et admet pour primitive la fonction 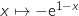 .
On a donc :
.
On a donc : 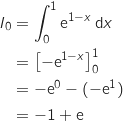
b. On admet que :
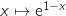 est définie et continue
sur
est définie et continue
sur 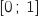 et admet pour primitive la fonction
et admet pour primitive la fonction 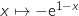 .
On a donc :
.
On a donc : 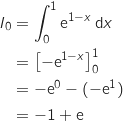
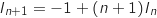
Dans le sujet original les élèves devaient établir cette relation grâce à un intégration par parties. Cette méthode
d'intégration n'est plus au programme à partir de la session 2013.
c. En déduire la valeur exacte de 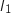 , puis celle de
, puis celle de 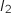 .
.
En utilisant la formule qu'on vient de montrer on a :
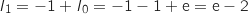
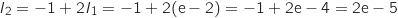
3. Calcul d'une aire plane
a. Etudier la position relative des courbes 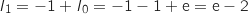
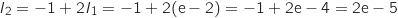
 et
et 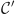 .
.
Pour étudier la position relative des courbes  et
et 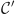 on étudie le signe de
on étudie le signe de 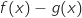 soit :
soit :
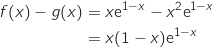 Pour tout
Pour tout  ,
, 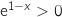 , donc le signe de
, donc le signe de
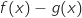 est le même que celui de
est le même que celui de 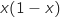 et on a directement
le tableau de signes :
et on a directement
le tableau de signes :

On en déduit que :
b. On désigne par  et
et 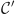 on étudie le signe de
on étudie le signe de 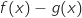 soit :
soit :
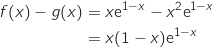 Pour tout
Pour tout  ,
, 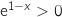 , donc le signe de
, donc le signe de
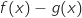 est le même que celui de
est le même que celui de 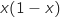 et on a directement
le tableau de signes :
et on a directement
le tableau de signes :

-
 est en dessous de
est en dessous de 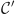 pour
pour 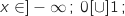 +
+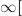 .
.
-
 est au dessus de
est au dessus de 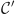 pour
pour 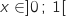 .
.
-
 et
et 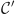 se coupent en
se coupent en 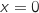 et en
et en  .
.
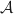 l'aire, exprimée en unité d'aire, de la partie du plan comprise d'une part entre les courbes
l'aire, exprimée en unité d'aire, de la partie du plan comprise d'une part entre les courbes  et
et 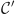 , d'autre part entre les droites d'équations respectives
, d'autre part entre les droites d'équations respectives 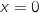 et
et 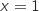 .
En exprimant
.
En exprimant 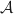 comme différence de deux aires que l'on précisera, démontrer l'égalité :
comme différence de deux aires que l'on précisera, démontrer l'égalité :
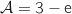
Compte tenu des positions de  et
et 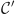 l'aire
l'aire 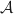 s'exprime par :
s'exprime par :
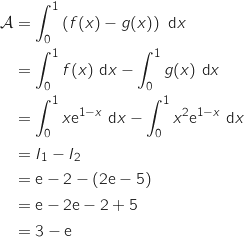
4. Etude de l'égalité de deux aires
Soit  et
et 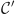 l'aire
l'aire 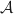 s'exprime par :
s'exprime par :
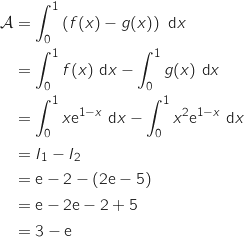
 un réel strictement supérieur à 1.
On désigne par
un réel strictement supérieur à 1.
On désigne par 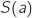 l'aire, exprimée en unité d'aire, de la partie du plan comprise d'une part entre les courbes
l'aire, exprimée en unité d'aire, de la partie du plan comprise d'une part entre les courbes  et
et 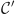 , d'autre part entre les droites d'équations respectives
, d'autre part entre les droites d'équations respectives 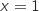 et
et 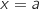 .
On admet que
.
On admet que 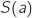 s'exprime par :
s'exprime par :
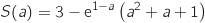
 pour laquelle les aires
pour laquelle les aires 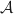 et
et 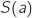 sont égales.
a. Démontrer que l'équation
sont égales.
a. Démontrer que l'équation 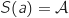 est équivalente à l'équation :
est équivalente à l'équation :
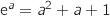 .
.
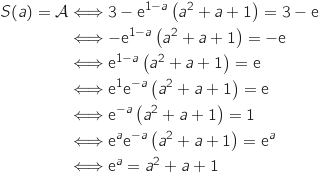
 , solution du problème posé.
, solution du problème posé.
Le problème est équivalent à résoudre l'équation 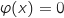 , avec
, avec 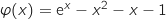 .
Cette fonction est définie et dérivable sur
.
Cette fonction est définie et dérivable sur 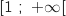 et on a
et on a 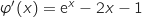 .
Pour étudier le signe de la dérivée on dérive une seconde fois :
.
Pour étudier le signe de la dérivée on dérive une seconde fois : 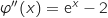 .
On a alors :
.
On a alors : 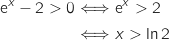 avec
avec 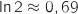 et donc
et donc 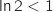 .
Du coup on a le tableau de variations de la fonction
.
Du coup on a le tableau de variations de la fonction 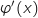 :
:
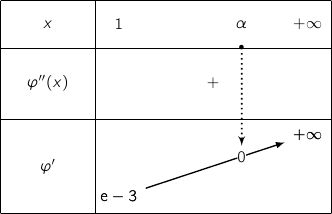
Avec 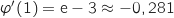 et
et 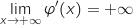 .
On en déduit d'après le tableau de variations qu'il existe un
unique réel
.
On en déduit d'après le tableau de variations qu'il existe un
unique réel  de
de 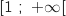 tel que
tel que 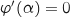 .
Avec la calculette, par balayage, on trouve
.
Avec la calculette, par balayage, on trouve 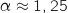 .
De tout ça, on déduit le signe de
.
De tout ça, on déduit le signe de 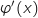 :
:
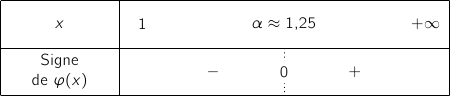
Au final on a le tableau de variations de  :
:
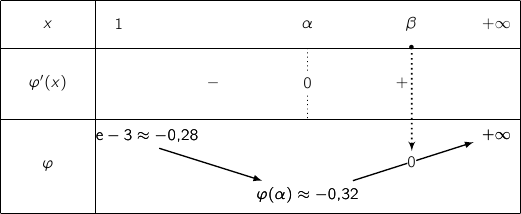
En utilisant le théorème des valeurs intermédiaires sur 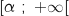 pour la fonction continue
pour la fonction continue  , strictement croissante, on prouve l'existence d'un
unique
, strictement croissante, on prouve l'existence d'un
unique 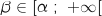 tel que
tel que 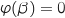 .
Par balayage avec la calculette, on trouve
.
Par balayage avec la calculette, on trouve 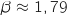 .
Donc il existe une unique valeur de
.
Donc il existe une unique valeur de  qui réponde au problème, c'est
qui réponde au problème, c'est 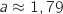 .
.
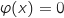 , avec
, avec 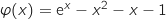 .
Cette fonction est définie et dérivable sur
.
Cette fonction est définie et dérivable sur 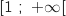 et on a
et on a 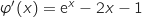 .
Pour étudier le signe de la dérivée on dérive une seconde fois :
.
Pour étudier le signe de la dérivée on dérive une seconde fois : 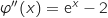 .
On a alors :
.
On a alors : 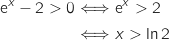 avec
avec 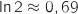 et donc
et donc 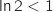 .
Du coup on a le tableau de variations de la fonction
.
Du coup on a le tableau de variations de la fonction 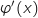 :
:

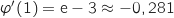 et
et 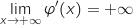 .
On en déduit d'après le tableau de variations qu'il existe un
unique réel
.
On en déduit d'après le tableau de variations qu'il existe un
unique réel  de
de 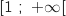 tel que
tel que 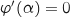 .
Avec la calculette, par balayage, on trouve
.
Avec la calculette, par balayage, on trouve 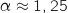 .
De tout ça, on déduit le signe de
.
De tout ça, on déduit le signe de 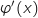 :
:

 :
:

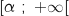 pour la fonction continue
pour la fonction continue  , strictement croissante, on prouve l'existence d'un
unique
, strictement croissante, on prouve l'existence d'un
unique 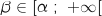 tel que
tel que 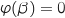 .
Par balayage avec la calculette, on trouve
.
Par balayage avec la calculette, on trouve 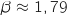 .
Donc il existe une unique valeur de
.
Donc il existe une unique valeur de  qui réponde au problème, c'est
qui réponde au problème, c'est 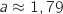 .
.
