Corrigé de l'exercice 1 du bac S de maths 2011 au Liban
Cacher les corrigés
Dans l'espace muni d'un repère orthonormal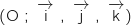 on donne les trois points :
on donne les trois points :
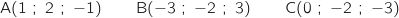
On calcule, par exemple, les coordonnées des vecteurs 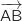 et
et 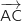 .
.
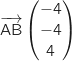
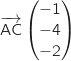 On remarque que les coordonnées des vecteurs ne sont pas proportionnelles, donc les vecteurs ne sont pas colinéaires et les points A, B et C ne sont pas alignés.
On remarque que les coordonnées des vecteurs ne sont pas proportionnelles, donc les vecteurs ne sont pas colinéaires et les points A, B et C ne sont pas alignés.
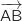 et
et 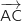 .
.
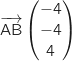
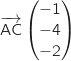 On remarque que les coordonnées des vecteurs ne sont pas proportionnelles, donc les vecteurs ne sont pas colinéaires et les points A, B et C ne sont pas alignés.
On remarque que les coordonnées des vecteurs ne sont pas proportionnelles, donc les vecteurs ne sont pas colinéaires et les points A, B et C ne sont pas alignés.
b. Démontrer que le vecteur
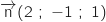 est un vecteur normal au plan (ABC).
est un vecteur normal au plan (ABC).
On calcule :
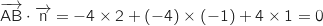
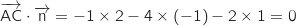 Donc le vecteur
Donc le vecteur  est orthogonal à deux vecteurs non colinéaires du plan (ABC), ce qui justifie que
est orthogonal à deux vecteurs non colinéaires du plan (ABC), ce qui justifie que  est normal au plan.
est normal au plan.
2. Soit 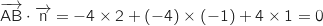
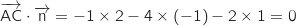 Donc le vecteur
Donc le vecteur  est orthogonal à deux vecteurs non colinéaires du plan (ABC), ce qui justifie que
est orthogonal à deux vecteurs non colinéaires du plan (ABC), ce qui justifie que  est normal au plan.
est normal au plan.
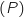 le plan dont une équation cartésienne est
le plan dont une équation cartésienne est 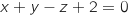 .
Démontrer que les plans (ABC) et
.
Démontrer que les plans (ABC) et 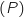 sont perpendiculaires.
sont perpendiculaires.
On lit directement sur l'équation du plan un vecteur normal : 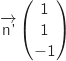 .
On calcule :
.
On calcule : 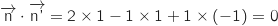 .
Donc des vecteurs normaux des plans sont orthogonaux ce qui prouve que (ABC) et
.
Donc des vecteurs normaux des plans sont orthogonaux ce qui prouve que (ABC) et 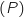 sont perpendiculaires.
sont perpendiculaires.
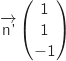 .
On calcule :
.
On calcule : 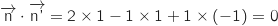 .
Donc des vecteurs normaux des plans sont orthogonaux ce qui prouve que (ABC) et
.
Donc des vecteurs normaux des plans sont orthogonaux ce qui prouve que (ABC) et 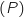 sont perpendiculaires.
sont perpendiculaires.
3.a. On appelle G le point de coordonnées
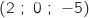 .
.
Dans le sujet original l'élève devait déterminer les coordonnées de G comme barycentre de points pondérés. Cette notion
n'est plus au programme à partir de la session 2013.
b. Démontrer que la droite (CG) est orthogonale au plan 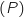 .
.
On calcule les coordonnées du vecteur : 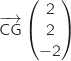 .
On remarque que
.
On remarque que 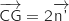 , donc
, donc 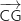 et
et 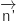 sont colinéaires
ce qui prouve que (CG) est orthogonale au plan
sont colinéaires
ce qui prouve que (CG) est orthogonale au plan 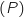 .
.
c. Déterminer une représentation paramétrique de la droite (CG).
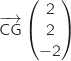 .
On remarque que
.
On remarque que 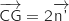 , donc
, donc 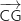 et
et 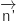 sont colinéaires
ce qui prouve que (CG) est orthogonale au plan
sont colinéaires
ce qui prouve que (CG) est orthogonale au plan 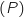 .
.
Un vecteur directeur de (CG) est 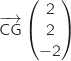 où encore en divisant par 2 :
où encore en divisant par 2 : 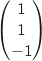 , de plus la droite
passe par C
, de plus la droite
passe par C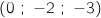 , donc on une représentation paramétrique de cette droite est :
, donc on une représentation paramétrique de cette droite est :
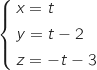
d. Déterminer les coordonnées du point H, intersection du plan 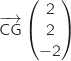 où encore en divisant par 2 :
où encore en divisant par 2 : 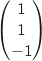 , de plus la droite
passe par C
, de plus la droite
passe par C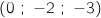 , donc on une représentation paramétrique de cette droite est :
, donc on une représentation paramétrique de cette droite est :
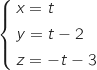
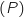 avec la droite (CG).
avec la droite (CG).
On doit résoudre le système :
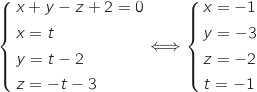 Donc H
Donc H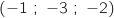
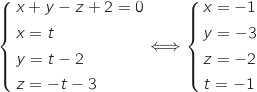 Donc H
Donc H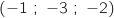
La fin de l'exercice portait sur des questions qui sont hors programme à partir de l'année scolaire 2012-2013.
