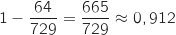Corrigé de l'exercice 2 du bac S 2011 de maths en Nouvelle-Calédonie
Cacher les corrigés
Chaque année, deux villages A et B organisent un concours sportif. Les concurrents tirent au sort un moyen de transport puis doivent relier le village A au village B le plus rapidement possible en utilisant ce moyen de transport et un parcours adapté. Pour le tirage, on utilise une urne contenant 4 jetons indiscernables au toucher. Sur un premier jeton figure la lettre V , sur le second la lettre R, sur le troisième la lettre P et sur le dernier la lettre L. Un concurrent tire au hasard un jeton :- s'il tire le jeton sur lequel figure la lettre V, il effectuera le trajet à vélo,
- s'il tire le jeton sur lequel figure la lettre R, il effectuera le trajet en roller,
- s'il tire le jeton sur lequel figure la lettre P, il effectuera le trajet à pied,
- s'il tire le jeton sur lequel figure la lettre L, il choisira librement son mode de transport parmi les trois précédents.
1. Construire un arbre pondéré correspondant à la situation.
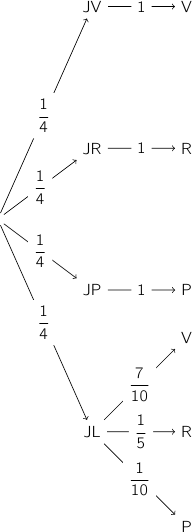
Pour les questions suivantes, on donnera les résultats arrondis au millième. 2. Calculer la probabilité qu'un concurrent effectue le trajet à vélo.
Calcul de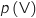 
Les événenements 
, 
, 
, 
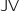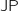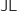constituent un système complet d'événements donc on a d'après la formule des probabilités totales :
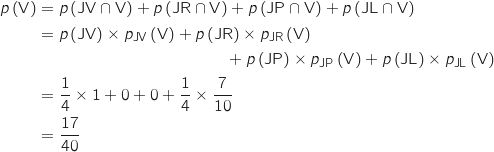
3. Sachant qu'un concurrent a effectué le trajet à vélo, quelle est la probabilité qu'il ait tiré le jeton sur lequel figure la lettre L ?
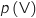Les événenements 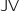, , , 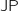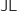constituent un système complet d'événements donc on a d'après la formule des probabilités totales :
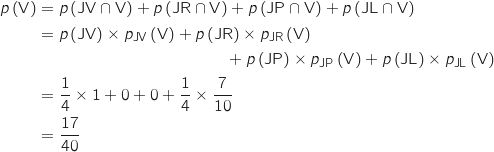
Calcul de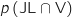 
D'après la formule des probabilités composées (principe multiplicatif sur l'arbre de probabilités) on a :
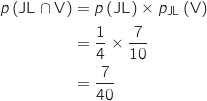Calcul de 
:
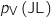On utilise la formule des probabilités conditionnelles :
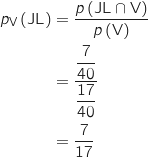
4. On admet que les résultats des différentes années sont indépendants les uns des autres.
L'expérience des années précédentes permet de considérer que la probabilité, pour le vainqueur, d'avoir effectué le trajet à vélo est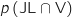
D'après la formule des probabilités composées (principe multiplicatif sur l'arbre de probabilités) on a :
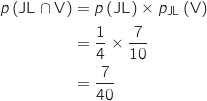Calcul de :
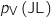On utilise la formule des probabilités conditionnelles :
.
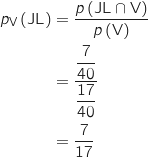
Calculer la probabilité qu'au cours des six prochaines années l'épreuve soit remportée au moins une fois par un concurrent « non cycliste ».
On considère l'expérience de Bernouilli dans laquelle la probabilité du succès est .
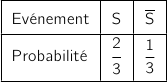
La loi associée à l'expérience est donnée dans le tableau ci-dessous :
On répète de façon indépendante 6 fois cette expérience, donc la variable aléatoire 
qui compte le nombre de succès suit une loi binomiale de paramètres 6 et .
L'événement « l'épreuve est remportée au moins une fois par un non cycliste » est le contraire de l'événement « l'épreuve est toujours remportée par un cycliste », c'est à dire «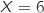 
».
La variable aléatoire suit la loi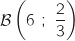 
, donc :
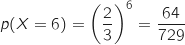Donc la probabilité de l'événement « l'épreuve est remportée au moins une fois par un non cycliste » est :
.
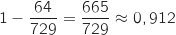
La loi associée à l'expérience est donnée dans le tableau ci-dessous :
qui compte le nombre de succès suit une loi binomiale de paramètres 6 et .
L'événement « l'épreuve est remportée au moins une fois par un non cycliste » est le contraire de l'événement « l'épreuve est toujours remportée par un cycliste », c'est à dire « ».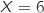
La variable aléatoire suit la loi 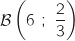, donc :
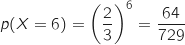Donc la probabilité de l'événement « l'épreuve est remportée au moins une fois par un non cycliste » est :
