Corrigé de l'exercice 4 du bac de maths S 2011 en Nouvelle-Calédonie
Cacher les corrigés
L'espace est rapporté à un repère orthonormal direct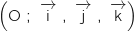 .
On considère les points A
.
On considère les points A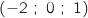 , B
, B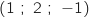 et C
et C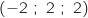 .
.
1.a. Calculer le produit scalaire
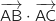 puis les longueurs AB et AC.
puis les longueurs AB et AC.
Coordonnées du vecteur 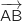 :
:
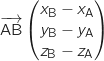
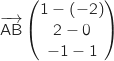
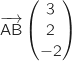 Coordonnées du vecteur
Coordonnées du vecteur 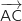 :
:
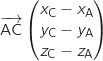
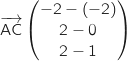
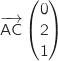
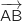 et
et 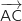 :
:
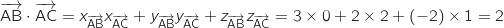 Norme du vecteur
Norme du vecteur 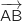 :
:
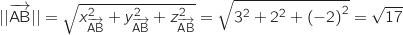 Norme du vecteur
Norme du vecteur 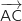 :
:
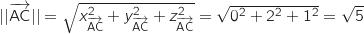 Donc AB=
Donc AB=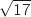 et AC=
et AC=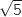 .
.
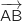 :
:
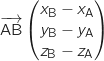
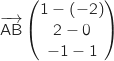
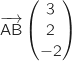 Coordonnées du vecteur
Coordonnées du vecteur 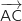 :
:
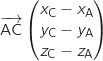
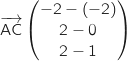
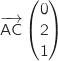
Produit scalaire de
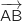 et
et 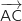 :
:
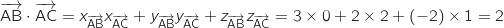 Norme du vecteur
Norme du vecteur 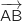 :
:
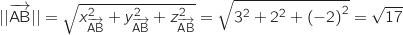 Norme du vecteur
Norme du vecteur 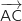 :
:
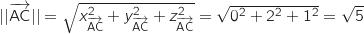 Donc AB=
Donc AB=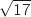 et AC=
et AC=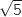 .
.
b. En déduire une valeur approchée arrondie au degré près de l'angle
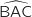 .
.
Le produit scalaire peut également s'écrire :
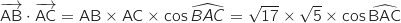 .
Donc
.
Donc 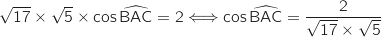 avec :
avec : 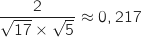 et
et 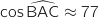 °.
°.
c. En déduire que les points A, B et C ne sont pas alignés.
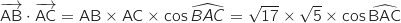 .
Donc
.
Donc 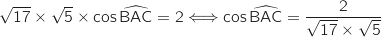 avec :
avec : 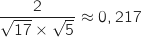 et
et 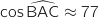 °.
°.
L'angle 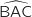 n'est ni nul, ni plat donc les points A, B et C ne sont pas alignés.
n'est ni nul, ni plat donc les points A, B et C ne sont pas alignés.
2. Vérifier qu'une équation cartésienne du plan (ABC) est : 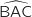 n'est ni nul, ni plat donc les points A, B et C ne sont pas alignés.
n'est ni nul, ni plat donc les points A, B et C ne sont pas alignés.
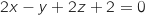 .
.
Les points 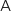 ,
, 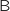 et
et 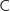 ne sont pas alignés, donc il définissent un plan.
Pour montrer que ce plan admet pour équation
ne sont pas alignés, donc il définissent un plan.
Pour montrer que ce plan admet pour équation
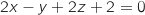 il suffit de vérifier que les coordonnées des 3 points vérifient l'équation en question :
Point
il suffit de vérifier que les coordonnées des 3 points vérifient l'équation en question :
Point 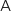 :
: 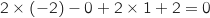 Point
Point 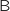 :
: 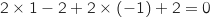 Point
Point 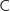 :
: 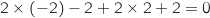 Donc une équation du plan considéré est bien
Donc une équation du plan considéré est bien 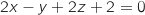 .
.
3. Soient 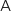 ,
, 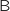 et
et 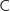 ne sont pas alignés, donc il définissent un plan.
Pour montrer que ce plan admet pour équation
ne sont pas alignés, donc il définissent un plan.
Pour montrer que ce plan admet pour équation
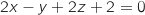 il suffit de vérifier que les coordonnées des 3 points vérifient l'équation en question :
Point
il suffit de vérifier que les coordonnées des 3 points vérifient l'équation en question :
Point 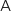 :
: 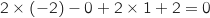 Point
Point 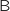 :
: 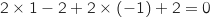 Point
Point 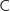 :
: 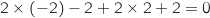 Donc une équation du plan considéré est bien
Donc une équation du plan considéré est bien 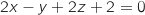 .
.
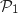 , et
, et 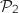 les plans d'équations respectives
les plans d'équations respectives 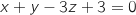 et
et
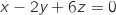 .
Montrer que les plans
.
Montrer que les plans 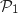 et
et 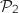 sont sécants selon une droite
sont sécants selon une droite  dont un système d'équations
paramétriques est
dont un système d'équations
paramétriques est 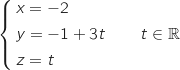
On résout le système :
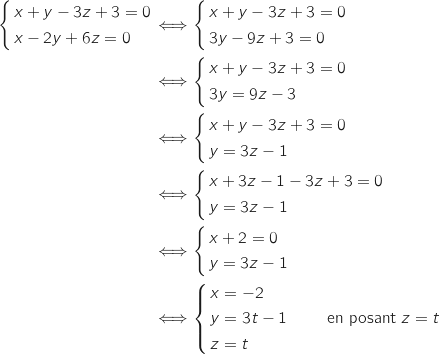 Donc les plans
Donc les plans 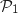 et
et 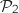 sont sécants selon la droite
sont sécants selon la droite  , dont on a obtenu une
représentation paramétrique ci-dessus.
, dont on a obtenu une
représentation paramétrique ci-dessus.
4. Démontrer que la droite 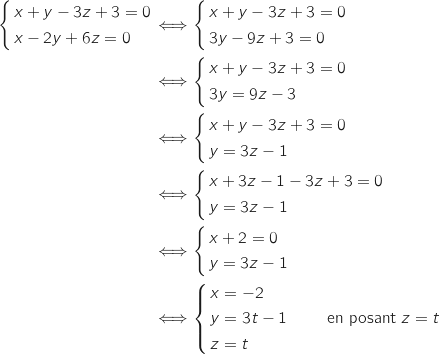 Donc les plans
Donc les plans 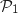 et
et 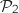 sont sécants selon la droite
sont sécants selon la droite  , dont on a obtenu une
représentation paramétrique ci-dessus.
, dont on a obtenu une
représentation paramétrique ci-dessus.
 et le plan (ABC) sont sécants et déterminer les coordonnées de leur point d'intersection.
et le plan (ABC) sont sécants et déterminer les coordonnées de leur point d'intersection.
On résout le système :
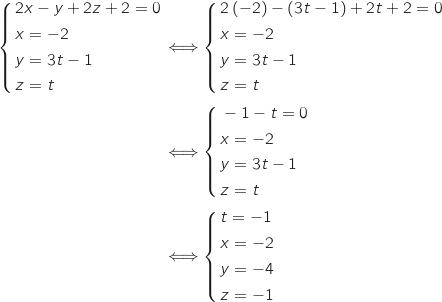 Donc la droite
Donc la droite  et le plan (ABC), se coupent au point de coordonnées
et le plan (ABC), se coupent au point de coordonnées 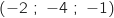 .
.
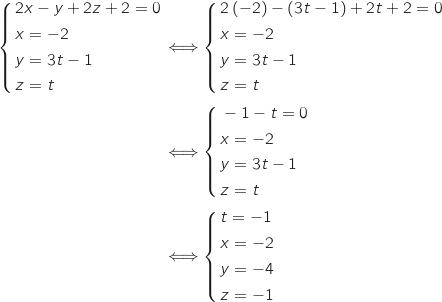 Donc la droite
Donc la droite  et le plan (ABC), se coupent au point de coordonnées
et le plan (ABC), se coupent au point de coordonnées 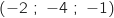 .
.
