Corrigé de l'exercice 1 du bac S de maths 2011 en Polynésie
Cacher les corrigés
Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse et donner une démonstration de la réponse choisie. Le plan complexe est muni d'un repère orthonormal direct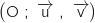 1. Soient A le point d'affixe
1. Soient A le point d'affixe 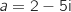 et B le point d'affixe
et B le point d'affixe 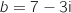 .
Proposition 1 : Le triangle OAB est rectangle isocèle.
.
Proposition 1 : Le triangle OAB est rectangle isocèle.
OA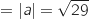 OB
OB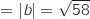 AB
AB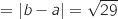 Le triangle est isocèle en A et
Le triangle est isocèle en A et 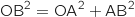 donc il est également rectangle en A
d'après la propriété de Pythagore.
donc il est également rectangle en A
d'après la propriété de Pythagore.
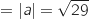 OB
OB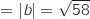 AB
AB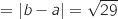 Le triangle est isocèle en A et
Le triangle est isocèle en A et 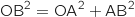 donc il est également rectangle en A
d'après la propriété de Pythagore.
donc il est également rectangle en A
d'après la propriété de Pythagore.
2. Soit
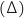 l'ensemble des points
l'ensemble des points 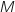 d'affixe
d'affixe  telle que
telle que 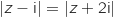 .
Proposition 2 :
.
Proposition 2 : 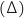 est une droite parallèle à l'axe des réels.
est une droite parallèle à l'axe des réels.
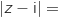 MA où A est le point d'affixe
MA où A est le point d'affixe 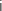 .
.
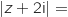 MB où B est le point d'affixe
MB où B est le point d'affixe 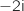 .
La condition s'écrit MA
.
La condition s'écrit MA MB donc les points M sont ceux de la médiatrice de [AB] qui est bien parallèle à l'axe des réels.
MB donc les points M sont ceux de la médiatrice de [AB] qui est bien parallèle à l'axe des réels.
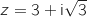 .
Proposition 3 : Pour tout entier naturel
.
Proposition 3 : Pour tout entier naturel  non nul,
non nul, 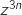 est imaginaire pur.
est imaginaire pur.
On calcule un argument de 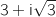 , on trouve :
, on trouve : 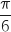 .
Donc
.
Donc 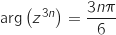 En prenant, par exemple,
En prenant, par exemple, 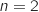 on a :
on a :
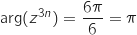 et dans ce cas
et dans ce cas 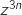 est un réel (et non un imaginaire pur).
est un réel (et non un imaginaire pur).
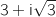 , on trouve :
, on trouve : 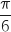 .
Donc
.
Donc 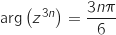 En prenant, par exemple,
En prenant, par exemple, 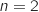 on a :
on a :
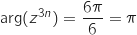 et dans ce cas
et dans ce cas 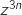 est un réel (et non un imaginaire pur).
est un réel (et non un imaginaire pur).
4. Soit
 un nombre complexe non nul.
Proposition 4 : Si
un nombre complexe non nul.
Proposition 4 : Si 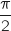 est un argument de
est un argument de  alors
alors 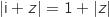 .
.
Si 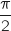 est un argument de
est un argument de  , alors
, alors 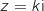 avec
avec 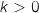 , donc on a :
, donc on a :
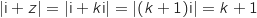
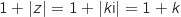 Donc l'égalité est bien vérifiée.
Donc l'égalité est bien vérifiée.
5. Soit 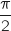 est un argument de
est un argument de  , alors
, alors 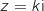 avec
avec 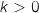 , donc on a :
, donc on a :
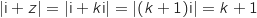
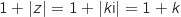 Donc l'égalité est bien vérifiée.
Donc l'égalité est bien vérifiée.
 un nombre complexe non nul.
Proposition 5 : Si le module de
un nombre complexe non nul.
Proposition 5 : Si le module de  est égal à 1 alors
est égal à 1 alors 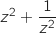 est un nombre réel.
est un nombre réel.
En posant 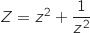 , on calcule
, on calcule 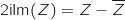 et on obtient 0.
Donc
et on obtient 0.
Donc 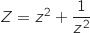 a sa partie imaginaire nulle, c'est donc un nombre réel.
a sa partie imaginaire nulle, c'est donc un nombre réel.
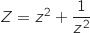 , on calcule
, on calcule 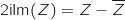 et on obtient 0.
Donc
et on obtient 0.
Donc 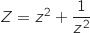 a sa partie imaginaire nulle, c'est donc un nombre réel.
a sa partie imaginaire nulle, c'est donc un nombre réel.
