Corrigé de l'exercice 2 du bac S de maths 2011 à Pondichéry
Cacher les corrigés
Partie I
Dans cette partie, ABCD est un tétraèdre régulier, c'est-à-dire un solide dont les quatre faces sont des triangles équilatéraux.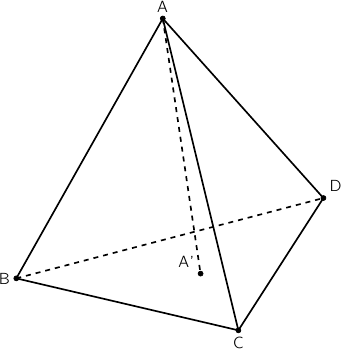
A' est le centre de gravité du triangle BCD. Dans un tétraèdre, le segment joignant un sommet au centre de gravité de la face opposée est appelé médiane. Ainsi, le segment [AA'] est une médiane du tétraèdre ABCD. 1. On souhaite démontrer la propriété suivante :
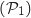 : Dans un tétraèdre régulier, chaque médiane est orthogonale à la face opposée.
a. Montrer que
: Dans un tétraèdre régulier, chaque médiane est orthogonale à la face opposée.
a. Montrer que 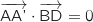 et que
et que 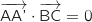 . (On pourra utiliser le milieu I du segment [BD] et le milieu J du segment [BC]).
. (On pourra utiliser le milieu I du segment [BD] et le milieu J du segment [BC]).
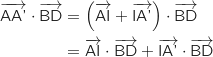 Comme ABD est équilatéral, la médiane (AI) est orthogonale à (BD), donc
Comme ABD est équilatéral, la médiane (AI) est orthogonale à (BD), donc 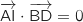 .
De même, BDC est équilatéral, donc la médiane (IA') est orthogonale à (BD) et
.
De même, BDC est équilatéral, donc la médiane (IA') est orthogonale à (BD) et 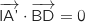 .
Finalement, on a bien
.
Finalement, on a bien 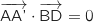 .
On montre exactement de la même façon, en utilisant le milieu J de [BC], que
.
On montre exactement de la même façon, en utilisant le milieu J de [BC], que 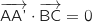 .
.
b. En déduire que la médiane (AA') est orthogonale à la face BCD. Un raisonnement analogue montre que les autres médianes du tétraèdre régulier ABCD sont également orthogonales à leur face opposée.
D'après la question précédente (produits scalaires nuls), la droite (AA') est orthogonale à (BD) d'une part et à (BC) d'autre part.
Ainsi (AA') est orthogonale à deux droites sécantes du plan (BCD) donc (AA') est orthogonale à (BCD).
Dans le sujet original on demandait de montrer une seconde propriété faisant intervenir la notion de
barycentre qui n'est plus au programme à partir de la session 2013 du baccalauréat.
Partie II
On munit l'espace d'un repère orthonormal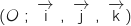 .
On considère les points P
.
On considère les points P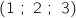 , Q
, Q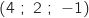 et R
et R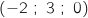 .
1. Montrer que le tétraèdre OPQR n'est pas régulier.
.
1. Montrer que le tétraèdre OPQR n'est pas régulier.
On a : 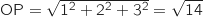 et
et
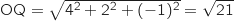 Donc deux côtés (au moins) du tétraèdre ne sont pas de même longueur, il n'est donc pas régulier.
Donc deux côtés (au moins) du tétraèdre ne sont pas de même longueur, il n'est donc pas régulier.
2. On admet que les coordonnées de P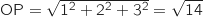 et
et
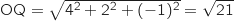 Donc deux côtés (au moins) du tétraèdre ne sont pas de même longueur, il n'est donc pas régulier.
Donc deux côtés (au moins) du tétraèdre ne sont pas de même longueur, il n'est donc pas régulier.
 , centre de gravité du triangle OQR sont :
, centre de gravité du triangle OQR sont :
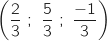
Dans le sujet initial les élèves devaient calculer les coordonnées de P'.
3. Vérifier qu'une équation cartésienne du plan (OQR) est : 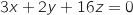 .
.
On remarque que les vecteurs 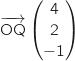 et
et
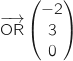 ne sont pas colinéaires (il n'existe pas
de coefficient de proportionnalité entre leurs coordonnées), donc O, Q et R définissent bien un plan.
On vérifie que les coordonnées de O, Q et R sastisfont l'équation proposée :
Pour O :
ne sont pas colinéaires (il n'existe pas
de coefficient de proportionnalité entre leurs coordonnées), donc O, Q et R définissent bien un plan.
On vérifie que les coordonnées de O, Q et R sastisfont l'équation proposée :
Pour O : 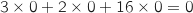 Pour Q :
Pour Q :
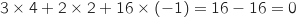 Pour R :
Pour R :
 Donc l'équation
Donc l'équation 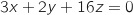 est bien une équation de (OQR).
est bien une équation de (OQR).
4. La propriété 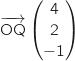 et
et
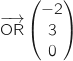 ne sont pas colinéaires (il n'existe pas
de coefficient de proportionnalité entre leurs coordonnées), donc O, Q et R définissent bien un plan.
On vérifie que les coordonnées de O, Q et R sastisfont l'équation proposée :
Pour O :
ne sont pas colinéaires (il n'existe pas
de coefficient de proportionnalité entre leurs coordonnées), donc O, Q et R définissent bien un plan.
On vérifie que les coordonnées de O, Q et R sastisfont l'équation proposée :
Pour O : 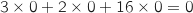 Pour Q :
Pour Q :
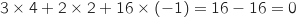 Pour R :
Pour R :
 Donc l'équation
Donc l'équation 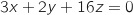 est bien une équation de (OQR).
est bien une équation de (OQR).
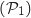 de la partie 1 est-elle vraie dans un tétraèdre quelconque ?
de la partie 1 est-elle vraie dans un tétraèdre quelconque ?
La médiane issue de P dans le tétraèdre a pour vecteur directeur :
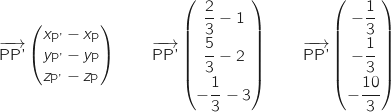 Un vecteur normal du plan (OQR) se lit directement sur son équation :
Un vecteur normal du plan (OQR) se lit directement sur son équation :
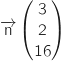 On remarque que
On remarque que  et
et 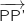 ne sont pas colinéaires
donc la droite (PP') n'est pas perpendiculaire au plan (OQR).
Ainsi on a un exemple de tétraèdre non régulier pour lequel
ne sont pas colinéaires
donc la droite (PP') n'est pas perpendiculaire au plan (OQR).
Ainsi on a un exemple de tétraèdre non régulier pour lequel 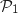 n'est pas vraie, donc on peut
dire que la propriété est fausse pour un tétraèdre quelconque.
n'est pas vraie, donc on peut
dire que la propriété est fausse pour un tétraèdre quelconque.
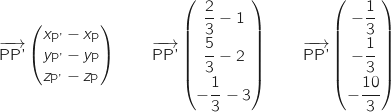 Un vecteur normal du plan (OQR) se lit directement sur son équation :
Un vecteur normal du plan (OQR) se lit directement sur son équation :
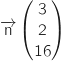 On remarque que
On remarque que  et
et 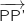 ne sont pas colinéaires
donc la droite (PP') n'est pas perpendiculaire au plan (OQR).
Ainsi on a un exemple de tétraèdre non régulier pour lequel
ne sont pas colinéaires
donc la droite (PP') n'est pas perpendiculaire au plan (OQR).
Ainsi on a un exemple de tétraèdre non régulier pour lequel 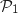 n'est pas vraie, donc on peut
dire que la propriété est fausse pour un tétraèdre quelconque.
n'est pas vraie, donc on peut
dire que la propriété est fausse pour un tétraèdre quelconque.
