Corrigé de l'exercice 3 du bac S de maths 2011 à Pondichéry
Cacher les corrigés
Un jeu consiste à lancer des fléchettes sur une cible. La cible est partagée en quatre secteurs, comme indiqué sur la figure ci-dessous.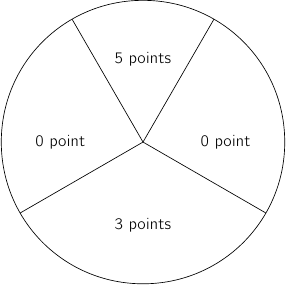
1. Le joueur lance une fléchette. On note
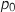 la probabilité d'obtenir 0 point.
On note
la probabilité d'obtenir 0 point.
On note 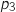 la probabilité d'obtenir 3 points.
On note
la probabilité d'obtenir 3 points.
On note 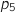 la probabilité d'obtenir 5 points.
On a donc
la probabilité d'obtenir 5 points.
On a donc 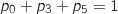 .
Sachant que
.
Sachant que 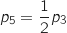 et que
et que 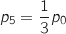 déterminer les valeurs de
déterminer les valeurs de 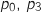 et
et 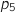 ·
·
On doit résoudre le système :
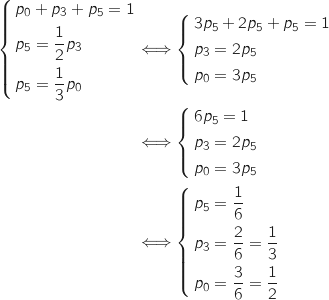
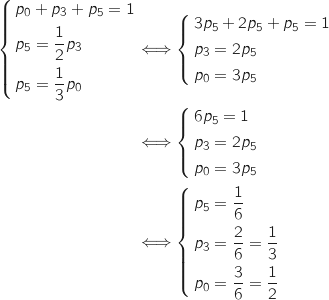
2. Une partie de ce jeu consiste à lancer trois fléchettes au maximum. Le joueur gagne la partie s'il obtient un total (pour les 3 lancers) supérieur ou égal à 8 points. Si au bout de 2 lancers, il a un total supérieur ou égal à 8 points, il ne lance pas la troisième fléchette. On note
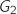 l'évènement : « le joueur gagne la partie en 2 lancers ».
On note
l'évènement : « le joueur gagne la partie en 2 lancers ».
On note 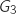 l'évènement: « le joueur gagne la partie en 3 lancers ».
On note
l'évènement: « le joueur gagne la partie en 3 lancers ».
On note 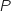 l'évènement: « le joueur perd la partie ».
On note
l'évènement: « le joueur perd la partie ».
On note 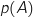 la probabilité d'un évènement
la probabilité d'un évènement 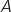 .
a. Montrer, en utilisant un arbre pondéré, que
.
a. Montrer, en utilisant un arbre pondéré, que 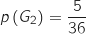 .
On admettra dans la suite que
.
On admettra dans la suite que 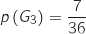
Dans l'arbre ci-dessous on n'a pas fait le 3 niveau qui est inutile pour répondre à la question.
niveau qui est inutile pour répondre à la question.
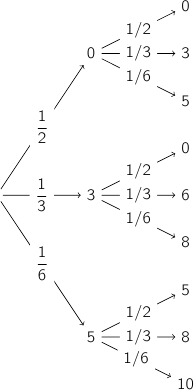
En utilisant le principe multiplicatif sur l'arbre pour les branches qui aboutissent à un total de points
supérieur ou égal à 8 on obtient :
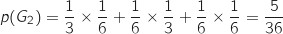 .
.
b. En déduire 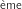 niveau qui est inutile pour répondre à la question.
niveau qui est inutile pour répondre à la question.

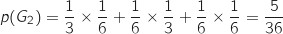 .
.
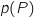 .
.
Le joueur ne peut pas gagner avec un seul lancer, il peut gagner en 2 ou 3 lancers, donc la probabilité
que le joueur gagne la partie est p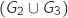 .
Les événements
.
Les événements 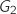 et
et 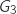 sont incompatibles (si le joueur gagne au deuxième lancer, la partie s'arrête) donc :
sont incompatibles (si le joueur gagne au deuxième lancer, la partie s'arrête) donc :
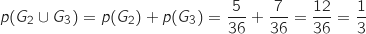 .
La probabilité de perdre (événement contraire) est :
.
La probabilité de perdre (événement contraire) est :
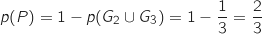 .
.
3. Un joueur joue six parties avec les règles données à la question 2.
Quelle est la probabilité qu'il gagne au moins une partie ?
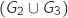 .
Les événements
.
Les événements 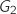 et
et 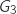 sont incompatibles (si le joueur gagne au deuxième lancer, la partie s'arrête) donc :
sont incompatibles (si le joueur gagne au deuxième lancer, la partie s'arrête) donc :
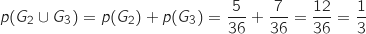 .
La probabilité de perdre (événement contraire) est :
.
La probabilité de perdre (événement contraire) est :
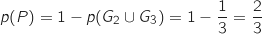 .
.
On considère l'expérience de Bernouilli dans laquelle la probabilité du succès est  (le joueur gagne la partie).
La loi associée à l'expérience est donnée dans le tableau ci-dessous :
(le joueur gagne la partie).
La loi associée à l'expérience est donnée dans le tableau ci-dessous :
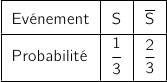
On répète de façon indépendante 6 fois cette expérience, donc la variable aléatoire 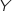 qui compte le nombre de succès suit une loi binomiale de paramètres 6 et
qui compte le nombre de succès suit une loi binomiale de paramètres 6 et  .
On cherche
.
On cherche 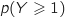 que l'on peut calculer plus facilement en prenant l'événément contraire :
que l'on peut calculer plus facilement en prenant l'événément contraire :
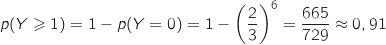 .
.
4. Pour une partie, la mise est fixée à 2 €.
Si le joueur gagne en deux lancers, il reçoit 5 €. S'il gagne en trois lancers, il reçoit 3 €. S'il perd, il ne reçoit rien.
On note  (le joueur gagne la partie).
La loi associée à l'expérience est donnée dans le tableau ci-dessous :
(le joueur gagne la partie).
La loi associée à l'expérience est donnée dans le tableau ci-dessous :

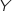 qui compte le nombre de succès suit une loi binomiale de paramètres 6 et
qui compte le nombre de succès suit une loi binomiale de paramètres 6 et  .
On cherche
.
On cherche 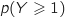 que l'on peut calculer plus facilement en prenant l'événément contraire :
que l'on peut calculer plus facilement en prenant l'événément contraire :
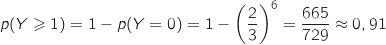 .
.
 la variable aléatoire correspondant au gain algébrique du joueur pour une partie. Les valeurs possibles pour
la variable aléatoire correspondant au gain algébrique du joueur pour une partie. Les valeurs possibles pour  sont donc:
sont donc: 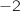 , 1 et 3.
a. Donner la loi de probabilité de
, 1 et 3.
a. Donner la loi de probabilité de  .
.
On a directement en utilisant les probabilités calculées avant :
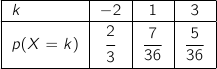
b. Déterminer l'espérance mathématique de 
 . Le jeu est-il favorable au joueur ?
. Le jeu est-il favorable au joueur ?
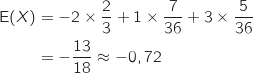 Donc le jeu est défavorable pour le joueur.
Donc le jeu est défavorable pour le joueur.
